Dispersion
des Mesures
Vous devez réaliser les
montages proposés et répondre individuellement
par écrit aux questions posées (si possible réaliser
le compte rendu sur traitement de texte). Mais, bien évidemment
vous notez – en plus – toutes les informations qui vous
semblent utiles : vous vous constituez
votre propre cours. |
Objectifs généraux
:
- Mettre en évidence les incertitudes de mesures et en déduire
l’écriture d’une valeur numérique
- Durée :1 séance
|
Matériel :
- 50 x R = 1 k

- Ohmètre + fiche technique
- Excel : dispersion.xls
- GBF
- 2 types différents de voltmètres
|
I Quelques questions ... |
 |
Classer les propositions suivantes en facteur positif ( P ), négatif (
N ) ou sans influence ( 0 ) sur la qualité d’une mesure :
- une seule mesure est suffisante :
- on n’utilise qu’un seul appareil de mesures :
- on recommence un grand nombre de fois la même mesure avec le même
appareil :
- on recommence un grand nombre de fois la même mesure avec différents
appareils :
- on refait la mesure en changeant de manipulateur :
- on prend l’appareil le plus cher :
- les conditions expérimentales varient ( température ambiante,
par exemple ) :
- on se fie à la notice du constructeur de l’appareil :
- on utilise un appareil à aiguille plutôt qu’un appareil digital
:
- l’utilisation du moyen de mesure est indépendante du manipulateur
:
Conclure sur les conditions d’une « bonne
» mesure.
II Mesure d'un échantillon de résistances
avec un ohmmètre. Premier cas : notion de dispersion
A) Objectif et travail à réaliser:
Nous utiliserons des résistances vendues par le fabricant comme étant
des résistances de valeur 1k connue à 5% près. Elles sont « livrées »
en bandes de 50 que l’on évitera de défaire pour réaliser
les mesures.
connue à 5% près. Elles sont « livrées »
en bandes de 50 que l’on évitera de défaire pour réaliser
les mesures.
Quel est l’encadrement prévu par le
fabricant pour les valeurs de ces résistances ? Il s’agit de déterminer
- la valeur moyenne des résistances
( en vérifiant qu’elle est bien à l’intérieur du 5%
prévu ).
- avec quel encadrement on peut connaître
cette valeur.
Vous mesurerez 50 résistances pendant que vôtre
binôme entrera les valeurs mesurées dans un fichier Excel préparé
à l’avance ; puis après échange avec le binôme
voisin, vous mesurerez 50 autres résistances : l’échantillon
mesuré par chaque binôme sera donc de 100 résistances.
On admettra que toutes les résistances mises à disposition
sont issues du même « lot » de fabrication.
On choisit de faire toutes les mesures avec un seul ohmmètre : Expliquer
ce qui, dans le paragraphe précédent, permet de justifier ce
choix.
Déterminer le nombre correct de chiffres
nécessaires à l’écriture de la valeur de cette résistance
compte tenu de l’encadrement ci-dessus. Justifier.
B) Manipulation
Dans le fichier Excel fourni dispersion.xls onglet « résistance
», il faut rentrer les valeurs mesurées les unes à la
suite des autres dans le tableau bleuté (une valeur de résistance
mesurée par case). Le second tableau permet de compter automatiquement
combien de valeurs ( leur effectif ) correspondent à une valeur fixée
de la grandeur mesurée.
Au fur et à mesure que le tableau de
valeurs mesurées se remplit, que peut-on dire de la répartition
de ces valeurs ?
On dit qu’il y a DISPERSION des mesures, ou encore fluctuations dues à
la grandeur mesurée ( ici R ).
Le tableur permet de représenter les
effectifs en fonction de chaque valeur ; écrire cette phrase en utilisant
d’autres mots
C) Exploitons ces résultats

|
La feuille Excel donne par calcul deux valeurs issues des mesures :
la moyenne et l’écart type 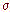 . .
L’écart type 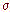 caractérise la dispersion des mesures : plus
caractérise la dispersion des mesures : plus 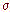 est petit, moins les valeurs sont dispersées ou plus elles sont
proches de la moyenne.
est petit, moins les valeurs sont dispersées ou plus elles sont
proches de la moyenne.
Les mathématiciens ( statisticiens ) ont montré que cette
représentation
avait un certain nombre de propriétés : 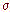 se lit de part et d’autre de la valeur moyenne sur la courbe.
se lit de part et d’autre de la valeur moyenne sur la courbe.
|
Compléter le tableau
suivant avec vos résultats et ceux des autres binômes (arrondir
arbitrairement à deux chiffres après la virgule les valeurs
données par Excel) :
Binôme |
1 |
2 |
3 |
etc |
Moyenne |
|
|
|
|
Écart-type |
|
|
|
|
Effectif à 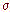 |
|
|
|
|
Effectif à 2 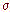 |
|
|
|
|
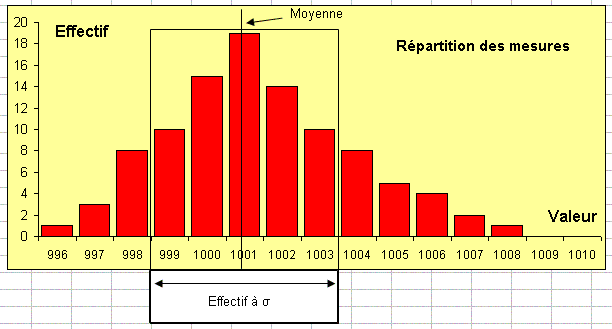
Les deux dernières lignes sont obtenues en totalisant les nombres
de fois qu’une valeur est obtenue ( effectifs ) dans une bande de largeur
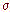 ou 2
ou 2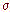 .
Par exemple le binôme 1 a obtenu 39 valeurs dans la bande de largeur
.
Par exemple le binôme 1 a obtenu 39 valeurs dans la bande de largeur
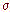 à gauche de
la moyenne et 26 valeurs dans la bande de largeur
à gauche de
la moyenne et 26 valeurs dans la bande de largeur 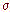 à droite de la moyenne. Effectif à
à droite de la moyenne. Effectif à 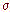 est 39 + 26. Recommencer pour une bande de largeur 2
est 39 + 26. Recommencer pour une bande de largeur 2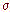 de chaque côté de la moyenne.
de chaque côté de la moyenne.
Déterminer l’encadrement obtenu pour
une largeur 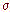 de chaque
côté
de chaque
côté
Déterminer l’encadrement obtenu pour
une largeur 2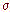 de chaque
côté
de chaque
côté
D) Conclusion
Écrire alors le résultat de cette
étude sous la forme R = Rmoyenne ± …... 
En vous interrogeant sur le nombre de chiffres
à conserver dans cette écriture : R =..........±...........
 Justifier.
Justifier.
Vérifier que cet encadrement respecte celui annoncé par le
fabricant des résistances.
III Mesure d'une seule résistance avec un seul
ohmmètre. Second cas : incertitude due à l’appareil de mesure
A) Utilisation de la documentation technique du multimètre
On se rend compte que plus les mesures sont nombreuses,
plus on a de « chances » d’approcher la vraie valeur … qui nous
restera inconnue ; mais cela prend du temps et ce n’est pas toujours possible
: pour contrôler qu’il y a bien 4,5 V aux bornes d’une pile, on ne va
pas faire 1000 fois cette mesure !
La solution vient du fabricant d’appareils de mesure qui
est tenu de tester son matériel : il va donc donner des indications
à l’utilisateur dans une notice technique le plus souvent en termes
d’incertitude relative exprimée en %.
Chercher dans la documentation technique du multimètre déjà
utilisé, de quoi compléter le tableau ci-dessous :
Calibre utilisé ( ohm )
|
|
% annoncé de la valeur affichée
|
|
Nombre de digits ou UR*
|
|
* N.B. Dans ces documentations techniques, on voit des données telles
que ± 0,3% de la valeur lue ± un digit ou une Unité de
Représentation (UR) : ce « digit » ou cette « UR
» est une unité correspondant au dernier chiffre affiché.
Exemple : 2 UR sur un affichage de 0,123 correspond à une incertitude
sur la mesure de ± 0,002.
B) Mesure de la valeur de la résistance
Utiliser l’une des résistances de 1 k utilisée précédemment ( sans l’extraire de la bande,
merci ).
utilisée précédemment ( sans l’extraire de la bande,
merci ).
Mesurer cette résistance et noter sa
valeur.
Calculer l’incertitude absolue notée 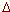 R d’après les renseignements trouvés dans la documentation
R d’après les renseignements trouvés dans la documentation
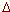 R =
R =
A partir de la mesure effectuée de cette résistance, donner
l’encadrement de la valeur de Rlue autorisé par la notice
du constructeur du multimètre : R = Rlue
± 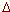 R soit :
R = .............±...............
R soit :
R = .............±............... 
Le calcul de 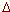 R justifie-t-il le choix fait préalablement de n’utiliser qu’un seul
ohmmètre pour effectuer cette mesure ?
R justifie-t-il le choix fait préalablement de n’utiliser qu’un seul
ohmmètre pour effectuer cette mesure ?
Cet encadrement est-il inclus dans celui trouvé
préalablement ? dans celui prévu par le fabricant ?
C) Conclusion
Quelles sont, d’après vous, les causes
d’incertitudes que met en évidence cette mesure ?
IV Mesure d'une seule tension avec plusieurs voltmètres.
Troisième cas : dispersion due aux appareils de mesure
A) Protocole expérimental
Vous devez mesurer la valeur U d'une tension alternative délivrée
par un GBF (d'environ 5 à 10 V) avec divers appareils pour lesquels
vous devrez choisir le calibre adapté sans oublier le choix de ~, AC
ou ACV ou efficace.
B) Mesures
La tension mesurée par un voltmètre « alternatif »
est nommée tension efficace et notée U ou Ueff.
Remplir le tableau ci-dessous
:
Appareil
|
Calibre |
Valeur mesurée |
Multimètre .........................
|
|
|
Multimètre .........................
|
|
|
C) Exploitation des mesures
Compléter le tableau ci-dessous avec
vos résultats et ceux des autres binômes ( noter
les valeurs telles qu’elles sont affichées par les voltmètres
) :
Binôme
|
1
|
2
|
etc
|
Multimètre ....................
|
|
|
|
Multimètre ....................
|
|
|
|
Dans le fichier Excel fourni « dispersion.xls »
onglet « tension », il faut entrer les valeurs ci-dessus dans
le tableau bleuté. Le second tableau permet de choisir un arrondi correct
au vu des mesures.
Le tableau des effectifs sert à compter automatiquement combien de
valeurs il y a dans chaque classe : le compléter en choisissant les
valeurs de sorte que l’histogramme soit centré.
Une classe est l’ensemble des valeurs comprises dans un
intervalle déterminé ( ici, par exemple, entre deux valeurs
consécutives comme 3,02 et 3,03 ).
L’écart type peut ne pas avoir de signification au
point de vue numérique, bien qu’il représente toujours la dispersion
des mesures, même si le nombre de classes est petit.
Cette dispersion des mesures
d’une même grandeur vous paraît-elle prévisible : donner
quelques raisons permettant d’interpréter ce résultat.
Écrire alors un encadrement de la mesure de cette
tension en vous interrogeant sur le nombre de chiffres à conserver
dans cette écriture : < U <
D) Conclusion
Toutes les mesures sont entachées d’erreurs pour les diverses raisons
examinées dans les trois cas précédents, ce qui fait
que le résultat en est généralement plus ou moins sûr
; en tout cas la valeur exacte ou vraie nous demeure inconnue.
Afin de préciser numériquement cette incertitude on écrit,
pour une grandeur A
A = Amesuré ± 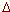 A et on nomme :
A et on nomme :
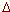 A l’incertitude
absolue ayant la même unité que la grandeur mesurée
A l’incertitude
absolue ayant la même unité que la grandeur mesurée- et
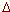 A / A l’incertitude
relative exprimée en %
A / A l’incertitude
relative exprimée en %
Exprimer les incertitudes relatives dans les
trois cas de mesures réalisées ci-dessus.
V Résumé
 |
Noter ci-dessous les définitions et conclusions importantes rencontrées
lors de cette séance |


