1. Ondes Sonore et ultrasonore
1. Caractériser
une onde sonore
Relier un GBF à
un haut-parleur. La fréquence du GBF sera de quelques centaines
de Hz.
Observer la vibration
de la membrane. Quel peut être l'effet de la membrane sur
l'air ambiant ? Faire apparaître sur un schéma la
direction de la déformation du milieu de propagation. L'onde
sonore est-elle longitudinale ou transversale ?
2. Mesure de la vitesse
de propagation d'une onde sonore
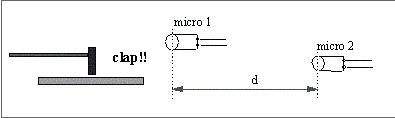
- On mesure directement
à l'aide d'un oscilloscope à mémoire la durée
de propagation d'un bruit bref ("clap") entre deux micros.
- Disposer les deux microphones
à environ 1 m l'un de l'autre, les relier respectivement
aux voies 1 et 2 de l'oscilloscope.
- Se placer en mode DUAL,
synchroniser sur la voie 1.
- Choisir une base de
temps convenable (le son parcourt 1 m en 3 ms)
- Décaler verticalement
de 2 ou 3 carreaux les traces 1 et 2
- Enfoncer STOR (le voyant
en haut à gauche s'allume)
- Enfoncer SINGLE
- Appuyer sur RESET :
un 2ème voyant s'allume, toute trace disparait de l'écran,
l'oscilloscope est en attente...
- Emettre un "clap"
en se plaçant sur la ligne des deux micros
- Les traces des signaux
délivrés par les micros apparaissent sur l'écran,
mesure
 .
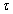- Faire l'expérience
pour 5 ou 6 distances d entre les micros.
- Tracer d en fonction
de 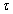. En déduire
la vitesse de propagation de l'onde sonore dans l'air.
- Donner un nom à
.
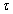L'onde sonore du "clap"
est-elle progressive? est-elle mécanique? est-elle périodique?
3. Étude de l'onde
ultrasonore
Dire pourquoi il est préférable
d’utiliser un générateurs d'ultrasons plutôt
qu'un haut-parleur.
- Alimenter l’émetteur
d’ultrasons et positionner le commutateur de l’émetteur
sur « Salve ».
- Relier les deux récepteurs
A et B aux entrées YA et YB d’un oscilloscope bicourbe.
Les positionner côte à côte face à l’émetteur.
- Régler l’oscilloscope
afin d’obtenir à l’écran le signal de
réception des salves par les deux récepteurs.
- Décaler verticalement
les deux courbes afin de pouvoir les distinguer (non superposables).
- Décaler le
récepteur B, dans la direction émetteur-récepteur,
d’une distance d suffisamment grande pour pouvoir mesurer
avec précision le retard ultrasonore
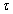entre les deux récepteurs.
- Organiser le dispositif
afin de réaliser les mesures les plus précises possibles.
- Afin de déterminer
précisément la célérité des ondes
ultrasonores, réaliser une série de 6 mesures précises
du retard ultrasonore
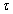pour différentes distances d.
- Tracer d en fonction
de 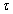. En déduire
la vitesse de propagation de l'onde sonore dans l'air.
L'onde ultrasonore est-elle
progressive? est-elle mécanique? est-elle périodique?
4. Détermination
de la célérité des ultrasons dans l’air
par la mesure d’une longueur d’onde, en mode “ Continu
”
- Positionner le commutateur
de l’émetteur sur le mode “ Continu ”.
- Placer de nouveau les
deux récepteurs en face de l’émetteur, au même
niveau, de façon à ce que les deux signaux soient
en phase.
- Régler l’oscilloscope
afin d’obtenir à l’écran deux signaux
superposables.
- Mesurer la période
et en déduire la fréquence des ultrasons.
- L’émetteur
étant fixé, lorsqu’on éloigne le récepteur
B du récepteur A, dans la direction émetteur-récepteurs,
les deux sinusoïdes se décalent. Sans tenir compte de
l’amplitude qui décroît pour le récepteur
B, les deux courbes “ se superposent ” à chaque
fois que la distance (récepteur A – récepteur
B) est un multiple entier de la longueur d’onde des ultrasons
dans l’air.
- Proposer un protocole
permettant de déterminer expérimentalement et de façon
précise la longueur d’onde des ultrasons.
- Mettre en œuvre
le protocole.
- Calculer la célérité
des ultrasons dans l’air. Compléter la feuille de réponses.
2.
Cuve à ondes
Faire les branchement
de la cuve à onde
1. Observation
d'onde circulaire ou curviligne et première question
- Choisir par exemple
la fréquence N = 25 Hz.
- Commenter la figure
obtenue ?
- Observer les rides
lumineuses rectilignes.
- À quoi correspondent-elles
?
- Pourquoi sont-elles
immobiles ?
- Ces rides lumineuses
sont elles équidistantes ? Pourquoi ?
- Avec la buse :
- Commenter l’aspect
de l’image lumineuse obtenue.
- Les rides lumineuses
sont-elles équidistantes ?
- Si la cuve n’et
plus horizontale, les rides sont-elles encore circulaires ? Selon
vous, à quoi est dû ce phénomène ?
2. Qu'arrivent-il quand
deux ondes se rencontrent?
Avec les deux buses :
Adapter la fréquence
et la puissance de sortie du GBF pour obtenir une figure de bonne
qualité. Une fréquence de l’ordre de 70 Hz donne
de bons résultats.
- Commenter l’image
obtenue ?
- Lorsque les ondes
se superposent sont-elles modifiées ?
- la célérité
des ondes change-t-elle ? En est-il de même lorsqu’un
projectile rencontre un obstacle ou un autre projectile ?
3. Mesure de
longueur d'onde et étude de la dispersion
- METHODE
DE MESURE DE LA LONGUEUR D’ONDE
-
Régler avec précision la fréquence N du
signal fourni par le GBF et mesurer à chaque fois la
longueur d’onde
des ondes progressives. Pour ce faire, disposer une règle
graduée sur le verre dépoli et repérer
les 2 rides lumineuses qui coïncident le mieux avec les
graduations de la règle et entre lesquelles on peut compter
un nombre n conséquent de longueurs d’ondes
- La
distance entre ces 2 rides étant égale à
D, en déduire la valeur de la longueur d’onde .
-
Effectuer les mesures pour les valeurs de N inscrites dans le
tableau ci-dessous et effectuer les calculs.
- La
longueur d’onde mesurée correspond-elle à
la réalité physique ?
- QUESTIONS
| N(Hz) |
15 |
20 |
25 |
30 |
35 |
etc |
| D
(cm) = n * |
|
|
|
|
|
|
| n |
|
|
|
|
|
|
| (cm)
= D/n |
|
|
|
|
|
|
| C(cm/s)
= *
N |
|
|
|
|
|
|
-
Quel intérêt voyez-vous à choisir une longueur
D contenant plusieurs ?
-
Comment varie
lorsque la fréquence augmente ?
-
Tracer rapidement le graphe C = f(N).
-
Comment varie la célérité C des ondes en
fonction de la fréquence N ?
-
Connaissez-vous un phénomène analogue dans un
autre domaine de la physique ?
4.Diffraction
- DIFFRACTION D’ONDES
RECTILIGNES PAR LE BORD D’UN OBSTACLE RECTILIGNE
- Disposer dans la
cuve un obstacle parallèle aux ondes rectilignes mais
qui n’obstrue que la moitié de la largeur de la
cuve.
- Fixer par exemple
la fréquence à 30 Hz et ajuster l’amplitude.
- Reproduire succinctement
la figure de diffraction obtenue. Pourquoi peut-on dire que
l’onde contourne les obstacles ?
- DIFFRACTION D’ONDES
RECTILIGNES ET QUESTIONS
- Disposer assez
près de l’émetteur d’ondes rectilignes
et parallèlement à celui-ci, 2 morceaux de plexiglas
de façon à créer une fente F de largeur
a voisine de 1 cm.
- Veiller à
ce que la cuve soit bien horizontale.
- Engendrer les
ondes rectilignes de fréquence voisine de 15 Hz, et travailler
en lumière stroboscopique.
- Comment se comporte
les ondes au-delà de la fente F ? Reproduire le schéma
de la figure obtenue sur votre copie.
- Au-delà
de la fente F la longueur d’onde
est-elle modifiée ?
- Lorsque la longueur
d’onde
est voisine de la largeur a de la fente indiquer l’allure
de la figure de diffraction au delà de la fente.
- Continuer à
augmenter la fréquence N des ondes. Ajuster éventuellement
l’amplitude. Comment évolue la figure de diffraction
lorsque N augmente ? Reproduire sur votre copie le schéma
de la figure observée.
- Lorsque
est beaucoup plus petite que a, le phénomène de
diffraction est-il encore très marqué ?
- Pour une fente
donnée de largeur a, conclure en indiquant pour quelle
valeur de
le phénomène de diffraction est le plus marqué
?
3.
Vidéo et simulation
1. Les ondes progressives
mécaniques
Ondoscope :
Le dispositif expérimental
est constitué par un ondoscope.
Comment varie
l'allure du signal au cours du déplacement.
- Mesures du retard temporel
et de la célérite :
- Pour chaque image,
à partir de t =0s on pointe pour deux abscisses séparées
de 0,50m la position de l’extrémité des tiges
de l’ondoscope pour 55 images. Ne pas oublier de faire l'étalonnage.
- Transporter les valeurs
dans Regressi en utilisant le presse papier.
- Superposer les ordonnées
Y1 et Y2 en fonction du temps.
- Déduire du
graphe le retard temporel entre les deux points considérés
et la célérité du signal sur l’ondoscope.
Croisement de
deux ondes dont l’élongation est opposée:
Que remarquez vous lorsque
les deux ondes se croisent ?
- Ouvrir ondoscopeCroisOndes.rw3
- Déduire du graphe
le retard temporel entre les deux points et la célérité
du signal sur l’ondoscope.
2. Ondes progressive
mécaniques périodiques : cuve à ondes
On
filme une onde périodique se propageant à la surface
de l’eau d’une cuve à ondes. La fréquence
des images vaut 25 images par seconde cuve2.avi
A l’aide du logiciel de pointage et du tableur grapheur "
REGRESSI " étudier la distance horizontale parcourue par
l’onde au cours du temps. Afficher la courbe x=f(t). La longueur
de la cuve fait 20 cm
- Déterminer la
vitesse de propagation de l'onde
- Déterminer la
période temporelle de l'onde
- En déduire la
longueur d'ondela longueur d’onde.
4.
Diffraction de la lumière
1. REFLECHIR : problème.
Il
a été dit en classe de 1°S : « Une onde se
propage en ligne droite »
alors :
1. Pourquoi suffit-il qu’une fenêtre soit à peine
entrouverte pour que le bruit extérieur pénètre
partout à l’intérieur d’une pièce
?
2. Pourquoi la nuit, lorsqu’on regarde une lumière à
travers un voilage très fin, observe-t-on une tache lumineuse
irisée formant une croix ?
Formuler, par une même phrase, le problème de physique
posé par les deux questions précédentes.
2. Ondes lumineuses.
MANIPULATION
On dispose d’un
laser, d’un écran (papier canson noir) percé de
petits trous de diamètres différents ou mieux d’un
diaphragme réglable, d’un écran d’observation.
- Proposer un protocole
pour répondre expérimentalement à la question.
Schématiser le montage.
- Rendre compte du phénomène
observé sur l’écran en faisant un dessin des
différentes figures observées.
- Le phénomène
est-il observable quel que soit le diamètre du trou ?
- Les figures de diffraction
sont–elles identiques quel que soit le diamètre du
trou ?
Remplacer le diaphragme
par une fente de largeur réglable
- Faire le schéma
de la figure de diffraction observée.
- Le phénomène
est-il observable quelle que soit la largeur de la fente ?
- Faire varier l’orientation
de la fente et dessiner la figure de diffraction correspondante
observée sur l’écran.
Répéter
l’expérience en remplaçant la fente par un obstacle
très fin (fil de pêche). Dessiner la figure de diffraction
observée.
- Faire le schéma
de la figure de diffraction observée.
- Faire varier l’orientation
du fil et dessiner la figure de diffraction correspondante observée
sur l’écran.
On dispose d’un
laser, de différentes fentes de largeurs connues montés
sous cache diapositives, d’un écran E dur lequel on fixe
une feuille de papier millimétrée pour effectuer les
mesures.
Réaliser le montage
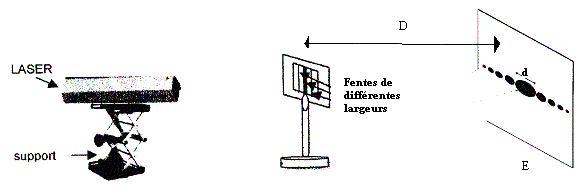
- Placer l’écran
d’observation E à une distance D de la fente la plus
grande possible (D>2m) ; on la maintiendra constante au cours
des mesures.
- Pour chaque fente de
largeur a, mesurer sur la figure de diffraction, la largeur d de
la tache centrale.
- Sachant que la largeur
de la tache centrale est le double de celle des autres taches, comment
procéder pour mesurer avec plus de précisions la longueur
d ?
- Répéter
l’expérience pour chaque fente (en maintenant constante
D).
- Mesurer la longueur
d que l'on notera "e" en remplaçant la fente par
un cheveu.
EXPLOITATION
avec Regressi
- Montrer, en traçant
la courbe représentant les variations de d = f(1/a), que
l’on peut écrire d = k /a (k constante).(Faire une
modélisation de la courbe)
- A partir de quelle
valeur de a peut-on dire que le phénomène de diffraction
n’est plus observable ?
- Déterminer la
valeur de k et la comparer au produit 2.
D (on donne
= nm)
- Montrer que l’on
a la relation
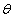= d / 2D. Si
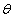est petit on peut écrire : tan
= (
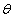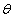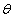est exprimé en radian).
- Créer la grandeur
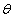
- Tracer la courbe
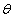= f(a). Faire une modélisation de la courbe.
- En déduire la
valeur e de l'épaisseur du cheveu
5.
Simulation (pour ceux qui s'ennuient)
|
