A. Propagation d’une onde ; ondes progressives

2. Ondes progressives mécaniques périodiques (2H)

CONTENUS

  • Notion d’onde progressive périodique.
    Périodicité temporelle, période; périodicité spatiale.
    Onde progressive sinusoïdale, période, fréquence, longueur d’onde; relation lamda= vT = v / f.
    La diffraction dans le cas d’ondes progressives sinusoïdales : mise en évidence expérimentale.
    Influence de la dimension de l’ouverture ou de l’obstacle sur le phénomène observé.
    La dispersion : mise en évidence de l’influence de la fréquence sur la célérité de l’onde à la surface de l’eau ; notion de milieu dispersif.

COMPÉTENCES EXIGIBLES

  • Reconnaître une onde progressive périodique et sa période.
    Définir pour une onde progressive sinusoïdale, la période, la fréquence, la longueur d’onde.
    Connaître et utiliser la relation lamda=v T, connaître la signification et l’unité de chaque terme, savoir justifier cette relation par une équation aux dimensions.
    Savoir, pour une longueur d’onde donnée, que le phénomène de diffraction est d’autant plus marqué que la dimension d’une ouverture ou d’un obstacle est plus petite.
    Définir un milieu dispersif.
    Exploiter un document expérimental (série de photos, oscillogramme, acquisition de données avec un ordinateur…) : détermination de la période, de la fréquence, de la longueur d’onde.
    Reconnaître sur un document un phénomène de diffraction.
  • Savoir-faire expérimentaux
    Réaliser un montage permettant de mettre en évidence le phénomène de diffraction dans le cas d’ondes mécaniques, sonores ou ultrasonores.
A chercher seul (corrigé)
A faire

 

1. Notion d’onde progressive périodique

1. Phénomène périodique

Un phénomène convenablement entretenu est périodique (ex : lame vibrante).
Un phénomène vibratoire est périodique lorsqu’il se reproduit identique à lui-même au bout d’un intervalle de temps T, appelé période. T s’exprime en secondes (s).

La fréquence d’un phénomène périodique est égale au nombre de périodes par seconde :

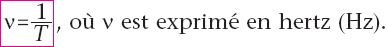
2. Onde progressive périodique

Une onde progressive est périodique si, à un instant quelconque, une photographie du milieu montre l’existence d’une périodicité spatiale de l’onde progressive. La perturbation se répète indéfiniment.
La période correspondante s’appelle longueur d’onde ; elle est notée .
Exemple : onde progressive dans un milieu à une dimension de direction de propagation [Sx).

3. Cas d'une vibration progressive sinusoidale

Une source vibratoire sinusoïdale (harmonique) génère une onde progressive sinusoïdale.
  • Vibration en phase
    Les points distants d’un nombre entier de longueurs d’onde sont dits en phase : d = k.    , avec k entier (ex : M1 et M2...).
 

 

  • Vibration en opposition de phase
    Les points distants d’un nombre impair de demi-longueurs d’onde sont dits en opposition de phase : d=(2k+1)/2, avec k entier (ex : M1 et M3).
    La figure représente des photographies, à différentes dates, d’une corde parcourue par une onde progressive sinusoïdale. La source vibratoire (S) vibre avec une période T.

4. Onde sonore

Les sons simples sont des ondes mécaniques sinusoïdales. Pour être audible, l'onde mécanique doit avoir une fréquence comprise entre 20 Hz et 20 kHz. Les ondes de fréquence supérieure à 20 kHz sont appelées ultrasons et celles de fréquence inférieure à 20Hz, infrason.

2. Double périodicité d’un phénomène ondulatoire ; équation aux dimensions

1. Périodicité temporelle T

Tous les points du milieu de propagation reproduisent le mouvement de la source ; ils vibrent avec la même période T et la même fréquence que la source. T est appelé « période temporelle » de l’onde progressive.

2. Périodicité spatiale

La longueur d’onde représente la période spatiale de l’onde : c’est la distance parcourue par l’onde pendant une période T (période du phénomène vibratoire entretenu).
L’expression de la longueur d’onde est :
avec : longueur d’onde en mètres (m), V : vitesse de propagation en mètres par seconde (m.s–1), T : période en secondes (s) et : fréquence en hertz (Hz).

3. Double périodicité et T

La période temporelle T est aussi bien la durée qu’il faut à l’onde pour avancer d’une longueur d’onde (période spatiale) que la durée nécessaire pour qu’un point se retrouve dans le même état de vibration.
La période spatiale est aussi bien la distance parcourue en T secondes (période temporelle) que la distance séparant deux points consécutifs vibrant en phase.

En pratique, pour mesurer la fréquence d’une onde sur cuve à onde par exemple, on utilise un stroboscope. La fréquence de l’onde est la plus petite fréquence stroboscopique pour laquelle il y a immobilité apparente.

4. Équation aux dimensions

La notion de dimension est rattachée à celle d’un type de grandeurs physiques ; elle est indépendante du système d’unités choisi.
Quatre dimensions indépendantes fondamentales permettent de décrire une grande partie de la physique :
– les longueurs symbolisées par la lettre L,
– les masses symbolisées par la lettre M,
– les temps symbolisés par la lettre T,
– les intensités des courants symbolisées par la lettre I.
En physique, l’utilisation du signe « = » signifie non seulement que les expressions de part et d’autre du signe ont la même valeur, mais aussi qu’elles sont de même nature, c’est-à-dire qu’elles ont la même dimension.
Par convention, la dimension d’une grandeur physique A (autre qu’une longueur, une masse, un temps ou une intensité) est notée [A].
La dimension d’un produit (ou d’un quotient) est le produit (ou le quotient) des dimensions. Les fonctions exponentielles, logarithmiques et trigonométriques n’ont pas de dimension.

5. Dimension de la longueur d’onde

D’après la définition de la longueur d’onde : [] =[V.T]=[V].[T]= L/T.T=L
La longueur d’onde a bien la dimension d’une longueur.

Ex 9 p.57

Ex 4/8 p.56

3. Phénomènes de diffraction et de dispersion

1. Diffraction des ondes progressives sinusoïdales
Lorsqu’on interpose un diaphragme de petite dimension dans le faisceau d’une onde progressive, le faisceau s’élargit : c’est le phénomène de diffraction. De manière générale, il y a diffraction chaque fois qu’une onde rencontre un obstacle .
Conséquences : les ondes peuvent contourner des obstacles.

2. Influence de la dimension de l’ouverture sur le phénomène observé

Lorsqu’une onde progressive sinusoïdale, de longueur d’onde , passe au travers d’une ouverture de dimension d :

  • si d ˜ ou d < , l’onde est diffractée et elle prend la forme d’une onde sphérique (ou circulaire) centrée sur l’ouverture ;
  • si d > , l’onde passe sans être perturbée. Elle est seulement diaphragmée (sauf près des bords où l’on retrouve une diffraction mais très négligeable en général).

Le passage par une ouverture, quelle que soit sa dimension d, ne modifie ni la longueur d’onde ni la fréquence de l’onde progressive.

Ex 11/14 p.57

Ex 15 p.58

Ex 11 p.57

Ex 17/18 p.58

Ex 22 p.59

3. Phénomène de dispersion des ondes mécaniques

Certains milieux sont très dispersifs : c’est le cas de la surface de l’eau.
Certains milieux sont très peu dispersifs : c’est le cas d’un gaz.
Un milieu est dit dispersif pour une onde progressive sinusoïdale si la célérité de l’onde dépend de sa fréquence.

Si le milieu n'est pas dispersif, chaque composante sinusoïdale de l'onde se propage avec la même vitesse et la forme de l'onde est conservée.

Objectif bac p.60/61/62