1. Caractère
aléatoire
Démarrer le logiciel
"Lancer de dés" et choisir le 1- "Caractère
aléatoire du lancer de dés"
- Sur la première
page, observer les résultats successifs obtenus lors du
lancer d'un dé. Faire au moins 100 lancers. Remettre à
zéro et recommencer au moins trois fois.
Que
pouvez-vous dire des probabilités d'obtention de l'un des
six résultats possibles ?
- Dans le menu "nombre
de dés", passer à 100 dés lancés
simultanément (avec remise) et observez le nombre de dés
qui affichent le résultat "6" lors de chaque
lancer de 100 dés.
Donnez un encadrement
approximatif du nombre de dés qui affichent "6"
lors de chaque lancer de 100 dés.
- Dans le menu "nombre de dés", passer au diagramme
en bâtons.
Dans cette partie on lance toujours 100 dés simultanément
(avec remise). Le diagramme représente, en abscisse, le
nombre de dés qui affichent "6" lors d'un lancer
de 100 dés et en ordonnée, la fréquence sortie
de ce nombre de dés.
Effectuez un grand nombre de lancers successifs de 100 dés
(attention à la modification automatique de l'échelle).
Quel
est le résultat le plus probable ?
Quelle est la moyenne des résultats ?
Cette moyenne était prévisible, montrez-le.
2. Suivi
de la décroissance d'une population
Quitter la partie en
cours (menu fichier) et choisir le 2- "Décroissance
du nombre de dés".
- Lancer de 200 dés
:
Dans un premier temps, on dispose de 200 dés identiques.
Lors de chaque lancer, le logiciel élimine les dés
qui affichent "6". Observer l'allure du nuage de points
obtenu.
Quelle est l'allure
de la courbe ?
Vers quelle valeur tend le nombre de dés restants lorsque
le nombre de lancer augmente ?
Pourquoi ?
- Lancer de 1000 dés
:
Dans le menu "nombre de dés", modifier le nombre
de dés pour passer à 1000 dés. Répéter
les opérations de lancer et observer l'allure du nuage
de points.
Que pouvez-vous
en dire (valeur de la limite, fluctuations…) ?
- Lancer de 1 000
000 de dés
Modifier le nombre de dés pour passer à 1 000 000
de dés. Observer que l'allure du nuage de points est toujours
la même mais que cette fois on n'observe pas de fluctuation.
Pourquoi ?
3. Etude
quantitative de la diminution de la population des dés
Garder le lancer de
1 000 000 de dés, remettre à zéro et préparer
un tableau dans lequel vous porterez : la date t du lancer (on effectue
par exemple un lancer chaque seconde) ; le nombre N(t) de dés
avant le lancer ; le nombre
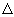 N(t)=N(t)-N(t+1)
de dés éliminés lors du lancer. Le tableau
doit avoir au minimum 15 lignes.
N(t)=N(t)-N(t+1)
de dés éliminés lors du lancer. Le tableau
doit avoir au minimum 15 lignes.
Compléter
votre tableau en calculant 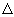 N(t)/N(t)
pour chaque lancer.
N(t)/N(t)
pour chaque lancer.
Votre tableau doit avoir l'allure ci-dessous :
Date
t du lancer |
N(t) |
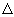 N(t) N(t) |
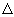 N(t)/N(t) N(t)/N(t) |
1 |
1
000 000 |
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
Que
pouvez-vous dire des diverses valeurs de 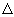 N(t)/N(t)
?
N(t)/N(t)
?
Quelle est la moyenne des valeurs obtenues, quel est son écart
type ?
Pourquoi cette moyenne est-elle négative ?
Pourquoi la valeur obtenue était-elle prévisible ?
On note 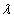 la valeur absolue de la moyenne.
la valeur absolue de la moyenne.
Quelle est, lors
de chaque lancer, la relation entre 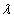 et
et 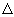 N(t)/N(t)
?
N(t)/N(t)
?
Rappel :L’écart
type 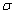 caractérise la dispersion des mesures : plus
caractérise la dispersion des mesures : plus 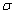 est petit, moins les valeurs sont dispersées ou plus elles
sont proches de la moyenne
est petit, moins les valeurs sont dispersées ou plus elles
sont proches de la moyenne 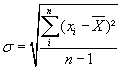
4. Application
à une population de noyaux radioactifs
La relation précédente
est établie pour une population de dés qui varie "par
à-coups" lors de chaque lancer. La proportionnalité
précédente, entre
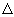 N(t)/N(t)
et
N(t)/N(t)
et 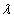 est valable
lors de chaque lancer.
est valable
lors de chaque lancer.
Pour une population de noyaux radioactifs la variation est proportionnelle
à la durée pendant laquelle on considère cette
variation. On note 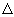 t
l'intervalle de temps entre deux déterminations du nombre
de noyaux.
t
l'intervalle de temps entre deux déterminations du nombre
de noyaux.
Quelle est alors
la relation entre 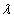 ,
, 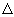 t et
t et  N(t)/N(t)
?
N(t)/N(t)
?