1. Le condensateur
1. Description - Symbole

|
Un
condensateur est formé de deux lames conductrices (armatures)
séparées par un isolant appelé diélectrique
(verre, air, film plastique, mica, céramique), dont la
représentation symbolique est donnée figure ci-contre.
Remarque : un condensateur
ne laisse pas passer de courant continu. |
2. Charges
des armatures

|
Dans
le circuit représenté sur la figure ci-contre,
le courant électrique qui circule provoque un déficit
d’électrons sur l’armature A et un excès
d’électrons sur l’armature B : le condensateur
se charge, et à chaque instant :

L’intensité
I du courant continu à travers une section (S) d’un
conducteur représente un débit constant de charges
électriques. Cette intensité est égale
à la valeur absolue de la charge électrique totale
traversant cette section par unité de temps : |
 |

3. Algébrisation
de l’intensité
Considérons un conducteur parcouru par un courant d’intensité absolue I dont on ne connaît pas, a priori, le sens réel. On oriente arbitrairement (dans un sens ou dans l’autre) le conducteur par une flèche dessinée sur le fil, ce qui définit l’intensité algébrique i.
Le sens choisi est appelé sens positif.
Si le sens réel du courant correspond au sens choisi, alors i = + I > 0.
Si le sens réel du courant correspond au sens inverse, alors i = – I < 0. |
4. Convention
récepteur
Dans le but de simplifier la relation liant la tension u et l’intensité i pour un dipôle passif, il faut se placer en convention récepteur.
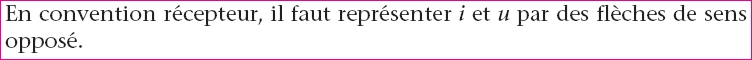

Dans un récepteur, le courant descend les potentiels. Si le dipôle AB est un récepteur, alors, pour u = uAB = VA – VB > 0 (soit VA > VB), le courant va bien de A vers B dans le dipôle, c’est-à-dire que i > 0. Les grandeurs tension et intensité sont, dans cette convention, de même signe.
Pour un générateur, et pour des raisons similaires, il faut utiliser la convention inverse (flèches u et i de même sens) appelée convention générateur.
|

|
Ex
6 p.146
|
|
|
2. Relation entre tension
et intensité
1. Charge d’un
condensateur à courant constant

|
Ex
7 p.146
|
|
|
2. Cas des courants variables

|
Dans ce cas, intensité
et tension sont des grandeurs qui sont des fonctions du temps.
On travaille alors avec les valeurs instantanées i(t) et
u(t).
Les lois fondamentales utilisées en courant continu (tensions,
intensités) restent valables pour des valeurs instantanées.
Dans le cas de courants variables, l’intensité n’est
plus un débit constant de charges. |
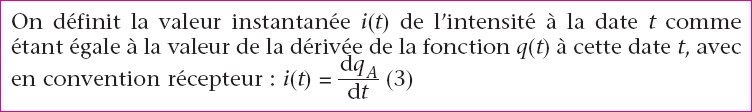
Comme qA(t) = C.uAB(t), alors 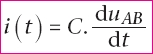 (4) (4)
|
3. Dipôle RC
1. Charge et décharge
d’un condensateur

|
Le
montage ci-contre est réalisé pour étudier
la charge puis la décharge d’un condensateur.
Le générateur de tension délivre ici une
tension continue, de valeur constante au cours du temps. On
utilise un oscilloscope à mémoire.
La charge ou la décharge d’un dipôle (R,
C) sont des phénomènes transitoires. |

Si
K passe en position (1), un courant positif s’établit
dans le circuit. L’intensité i de ce courant
décroît progressivement tandis que uC augmente.
Quand uC = Uo, alors i = 0.
D’après la loi des mailles :
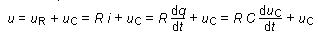 donc
donc
 (5)
(5)
Cette
équation est l’équation différentielle
régissant la charge du
condensateur.
Solution
analytique
Vérifions
que la solution analytique uC=Aeat+B satisfait
à l'équation.
En remplaçant dans (5), uC et sa dérivée
par leur expression, on obtient :
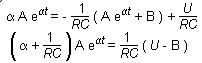
Les
deux membres de cette équation ne peuvent être
égaux, quelle que soit la valeur de t, que s'ils sont
nuls ; A ne pouvant être nul, on a

La
solution satisfaisant à l'équation différentielle
de la charge est :
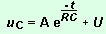
Prise
en compte des conditions initiales
Elles
permettent de déterminer la constante A. A t=0, le
condensateur n'est pas chargé, la tension uC est nulle.
On peut écrire :
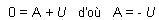
Lors
de la charge, la tension aux bornes du condensateur a pour
expression :
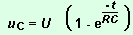
On
en déduit celles de la charge q du condensateur et
de l'intensité i du courant dans le dipôle RC,
en fonction du temps :
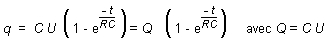
Pa
dérivation, on obtient :
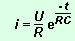
|

Si
K passe de (1) à (2), un courant négatif s’établit
dans le circuit. La valeur absolue de l’intensité
de ce courant décroît : le condensateur se décharge.
Quand i = 0 alors uC = 0.
D’après la loi des mailles :
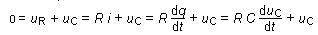
 (6)
(6)
Cette
équation est l’équation différentielle
régissant la décharge du condensateur.
Solution
analytique
Vérifions
que la solution analytique uC=Aeat+B satisfait
à l'équation.
En remplaçant dans (6), uC et sa dérivée
par leur expression, on obtient :
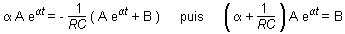
Les
deux membres de cette équation ne sont égaux,
quelle que soit la valeur de t que s'ils sont nuls. On a donc
:
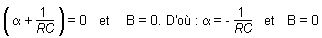
La
solution satisfait à l'équation différentielle
de décharge :
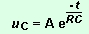
Prise
en compte des conditions initiales
Elles
permettent de déterminer la constante A. A t=0, le
condensateur est chargé, la tension uC est égale
à U. On peut écrire U=A.
Lors
de la décharge, la tension aux bornes du condensateur
a pour expression :
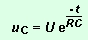
On
en déduit celles de la charge q du condensateur et
de l'intensité i dans le dipole RC :

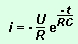
|
 |
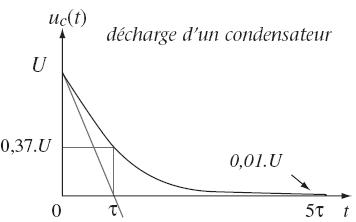
Remarque
: En pratique, on admet que la charge est termineée lorsque
la tension uC aux bornes du condensateur atteint 99% de sa valeur
finale théorique. Cette valeur est atteinte pour une durée
de charge voisine de 5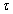 . .
De même, la décharge est considérée
comme terminée au bout d'une durée voisine de 5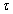 . .
|
2. Influence de la constante
de temps 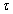 sur
la charge et la décharge sur
la charge et la décharge
On remplace le générateur de tension continue par un générateur délivrant une tension en créneaux. Les résistance et condensateur
sont variables.
Sur la voie B, on observe la tension aux bornes du condensateur. On fait varier les valeurs des résistances du conducteur ohmique et la capacité du condensateur. On obtient les deux oscillogrammes de la figure ci-dessous :
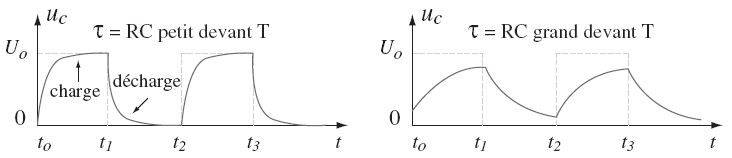
|

|
Ex
11 p.147
|
 |
Ex
10 p.147 |
4. Intensité et
énergie dans un condensateur
1. Intensité du
courant lors de la charge et la décharge
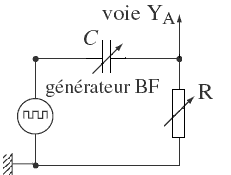
|
Pour
étudier l’intensité du courant, l’oscilloscope
doit être branché aux bornes du conducteur ohmique
. On visualise ainsi la tension
uR = R.i, donc l’intensité du courant à
un facteur R près.

|
Intensité lors de la charge :
D’après (4) et (5), on a 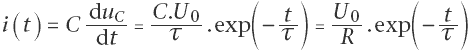
En posant 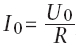 , on a , on a 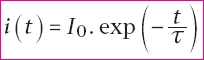
i(t) est une fonction décroissante par valeurs positives.
Intensité lors de la décharge :
De même, d’après (4) et (6), on a :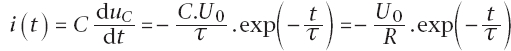
On obtient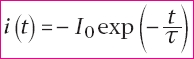
i(t) est une fonction croissante par valeurs négatives.
Contrairement à uC(t), i(t) est discontinue.
|

|
Ex
17 p.149
|
 |
Ex
14/15 p.148 |
2. Énergie stockée
dans un condensateur
Un condensateur chargé constitue un réservoir d’énergie. Cette énergie peut être restituée dans un circuit (principe du flash photographique).
La valeur de l’énergie potentielle électrostatique stockée par un condensateur est :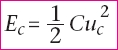
D’après (2), on a aussi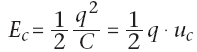
Remarque : stockage et déstockage de l’énergie ne peuvent jamais s’effectuer instantanément, ce qui confirme que les variations de la tension uC(t) ne sont jamais discontinues.
|
3. Analyse dimensionnelle
de la constante de temps 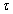

|
Ex
12/16 p.148
|
 |
Ex
19 p.150 |
Objectif bac p.152/153/154
|