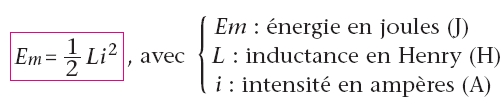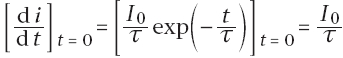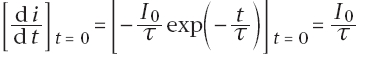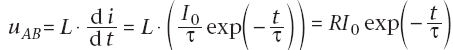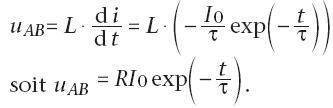1. La bobine
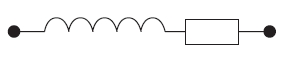
1. Description - Symbole
|
Les
bobines ou inductances sont constituées d’un fil
conducteur isolé bobiné sur un support isolant
(bakélite, téflon...) cylindrique ou torique,
à l’intérieur desquelles on peut introduire
des noyaux métalliques (alliage ferromagnétique)
ou des noyaux de ferrite.
Du point de vue électrique, une bobine est caractérisée
:
– par une grandeur appelée inductance, notée
L, exprimée en henry (H) ;
– par sa résistance r exprimée en ohm qui
représente son défaut.
Remarque : l’inductance dépend des caractéristiques
physiques de la bobine (nombre de spires par unité de
longueur, présence ou non d’un noyau...).
|
2. La bobine
en convention récepteur

|
La
tension aux bornes d’une bobine est :
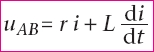 (1). (1).
Le terme r.i correspond à la tension que l’on aurait
aux bornes d’un
conducteur ohmique de résistance r.
Le terme  est lié aux variations de l’intensité du
courant dans la
est lié aux variations de l’intensité du
courant dans la
bobine.
En particulier, si i > 0 et tend à augmenter (lors
de la fermeture du circuit) alors  >
0. La bobine se comporte bien en récepteur qui s’oppose
au passage du courant, elle modère l’augmentation
de i. >
0. La bobine se comporte bien en récepteur qui s’oppose
au passage du courant, elle modère l’augmentation
de i.
Inversement, si i > 0 et tend à diminuer (lors de
l’ouverture du circuit), alors  <
0. La bobine se comporte en générateur qui tend
à maintenir un courant dans le circuit. <
0. La bobine se comporte en générateur qui tend
à maintenir un courant dans le circuit.
|
Remarque : en régime permanent et en courant continu (i = cte), on a uAB = ri ; la bobine se comporte alors comme un simple conducteur ohmique.
|
3. Énergie
dans une bobine
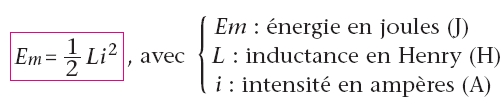

|
Ex
12 p.170
|
|
|
2. Dipôle RL
1. Étude expérimentale
|
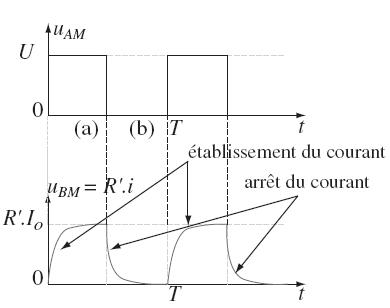
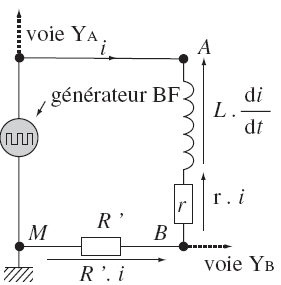
On visualise la
tension aux bornes du générateur sur la voie
YA de l’oscilloscope.
On visualise la tension uBM aux bornes du conducteur
ohmique R’ (à un coefficient près, c’est
l’intensité i du courant dans le circuit : uBM
= R' i ) sur la voie YB
On obtient les
oscillogrammes dessinés sur le schéma ci-contre.
On voit que :
(a) lors de la mise sous tension du circuit, le courant n’atteint
pas immédiatement son maximum ;
(b) lorsque la tension s’annule, le courant ne diminue
que progressivement.
|
2. Étude des phénomènes
transitoires
L’interrupteur
K du montage précédent étant fermé,
un courant i(t) s’établit dans le circuit.
D’après
la loi d’additivité des tensions : uAM = uAB
+ uBM.
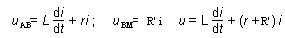
En
posant R = r + R', On obtient :
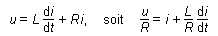 (2) (2)
C’est
l’équation différentielle régissant
l’établissement du courant dans la bobine.
Durant l’établissement
du courant, le générateur maintient une tension
constante : uAM = U. vérifions que la solution :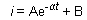
satisfait
à l'équation différentielle (2). En remplaçant
i et sa dérivée par leur expression, on a :
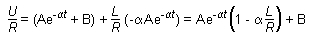
d'où
: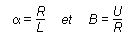
La
solution 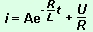 satisfait à l'équation différentielle
du circuit lorsque le dipôle RL est soumis à
la tension constante U.
satisfait à l'équation différentielle
du circuit lorsque le dipôle RL est soumis à
la tension constante U.
Etablissement
du courant
A
l'instant de date t=0, on ferme le circuit. La tension aux
bornes du dipôle RL devient égale à U.
On a donc : 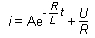
Lorsque
t devient très grand, l'intensité du courant
devient constante : le régime permatnent est atteint.
En notant I cette instensité qui a pour valeur U/R
: 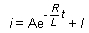
A
t=0, l'intensité du courant est nulle : 0=A+I, d'où
A=-I. On a donc :
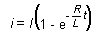
|
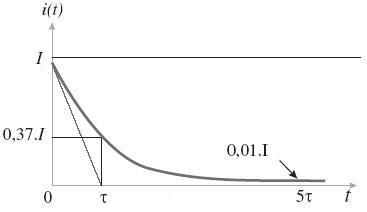
On
ouvre l’interrupteur du montage précédent
: le courant décroît progressivement jusqu’à
la valeur 0.
D’après
la loi d’additivité des tensions : uAM = uAB
+ uBM,
soit :
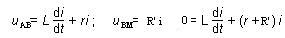
En
posant R = r + R'On obtient l’équation différentielle
:
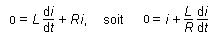 (3) (3)
C’est
l’équation différentielle régissant
l’annulation du courant
dans la bobine.
Si
t=0 est la date à laquelle on ouvre le circuit, alors
pour t>0, u=0 et on a donc :
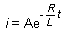
A
t=0, i=I donc A=I
Lors
de la rupture du courant dans le dipôle RL, la valeur
de l'intensité est donnée par :
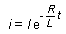
|

|
Ex
10/11 p.170
|
 |
Ex
9 p.170
Ex 16/17
p.171 |
3. Constante de temps 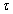 et
tension pour un circuit RL
et
tension pour un circuit RL
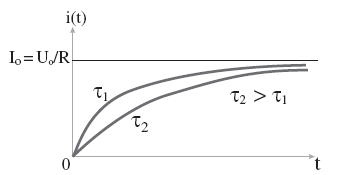
1. Influence des paramètres
R et L
|
L’établissement
du courant et son arrêt dans le circuit sont d’autant
plus rapides que la constante 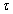 = L /R est plus petite, c’est-à-dire que L est
petit et R est grand
= L /R est plus petite, c’est-à-dire que L est
petit et R est grand |
2. Détermination
expérimentale de la constante de temps 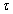 = L/R
= L/R
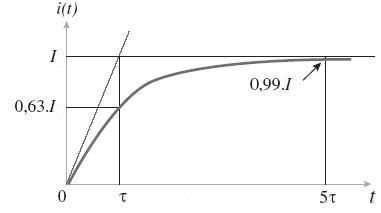
Le coefficient directeur de la tangente à la courbe i(t) au point d’abscisse t = 0 est égale à la valeur de la dérivée de la fonction i(t) à la date t = 0.
Dans le cas de l’établissement du courant dans le circuit et d’après (X) on a :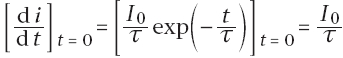
Dans le cas de l’annulation du courant dans le circuit et d’après (Y), on a :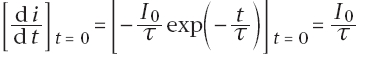
Dans les deux cas, le coefficient directeur de la tangente à la courbe i(t) au point d’abscisse t = 0 permet la détermination facile de la constante de temps 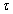 . .
Remarque : 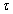 = L/R a la dimension d’un temps et s’exprime donc en secondes. = L/R a la dimension d’un temps et s’exprime donc en secondes.
|

|
Ex
18 p.172
|
 |
Ex
20 p.172 |
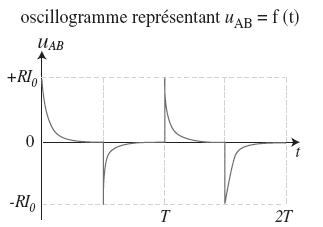
3. Évolution de
la tension en régime transitoire
|
Lors de l’établissement
du courant, et d’après (1) et (X), si la résistance
de la bobine est négligeable, on a :
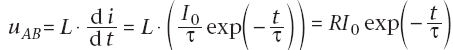
Lors
de l’arrêt du courant, et d’après (1)
et (Y), si la résistance de la bobine est négligeable,
on a :
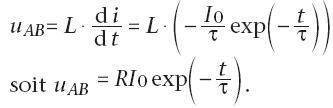
Remarque
: on observe que la variation de la tension est discontinue.
|
|
|
 |
Ex
15 p.171 |
Objectif bac p.174
|
= L/R


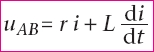 (1).
(1).
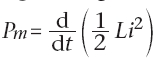 (4).
(4).