1. Vecteur vitesse
1. Système
On appelle système, un objet ou ensemble d’objets que l’on distingue de son environnement pour en faire l’étude. Un système est indéformable si la distance entre deux quelconques de ses points reste constante au cours du temps ; un tel système est appelé « solide ».
On définit le centre de masse d’un système comme étant le point remarquable où l’on peut imaginer avoir concentré toute la matière du système, dans le cas où, pour une étude simplifiée, ce système devrait être réduit à un point. Dans le cas d’un solide homogène, le centre de masse est situé au centre géométrique du solide.
|
2. Référentiels
Un objet peut être en mouvement par rapport à un observateur et immobile par rapport à un autre. Pour définir le mouvement d’un objet, il est nécessaire de préciser le référentiel d’étude et le repère de temps.
Un référentiel est le solide ou tout point du solide par rapport auquel on décrit le mouvement d’un mobile. Exemple : le référentiel terrestre (la Terre, le sol, le laboratoire...).
À ce référentiel, on associe en général un repère d’espace comportant 1, 2 ou 3 vecteurs unitaires  et un point origine O lié au référentiel. et un point origine O lié au référentiel.
Pour définir la position d’un objet dans le temps, il est nécessaire de définir un repère de temps. Ce repère est constitué d’un instant ou d’une date origine t0 (début de l’expérience ou de l’observation par exemple) et d’une unité de durée. Dans le système international (S.I.), l’unité de temps est la seconde (s).
Tout point M de l’espace est alors repéré, à une date t, par le vecteur position :

Dans un repère orthonormé, la distance (OM) est alors égale à : 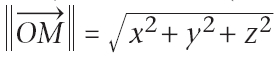
Dans le système international (SI), elle s’exprime en mètre (m).
|
3. Vecteur
vitesse
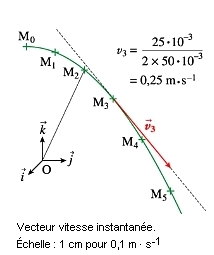
|
Entre
les instants t et t +  t,
le mobile se déplace de M en M’ suivant un vecteur
déplacement t,
le mobile se déplace de M en M’ suivant un vecteur
déplacement 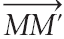 qui correspond à une variation du vecteur position :
qui correspond à une variation du vecteur position :

La
vitesse instantanée est définie comme étant
le taux de variation de la position par rapport au temps, pour
une durée  t
la plus petite possible : t
la plus petite possible :

Le
vecteur vitesse est égal à la dérivée
du vecteur position par rapport au temps ; il est tangent à
la trajectoire, dans le sens du mouvement. Dans un repère
fixe 

|
La valeur de la vitesse est 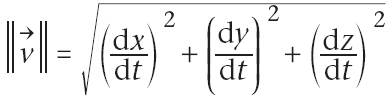
Dans le système international, elle s’exprime en mètre par seconde (m.s-1).
|
2. Première et troisième
lois de Newton
1. Forces
On appelle force toute action mécanique d’un corps sur un autre capable de produire des effets sur le mouvement ou la forme de ce dernier corps.
Si une force est exercée par un autre point ou objet du système lu-imême, il s’agit d’une force intérieure. Si une force est exercée par un objet ou un point extérieur au système, il s’agit d’une force extérieure.
Parmi les forces extérieures, on peut distinguer :
– les forces de contact : le corps qui subit la force est en contact avec celui qui la crée (réaction d’un support, forces de frottement, tension d’un fil...). Les forces de contact peuvent être localisées en un point ou réparties sur la surface de contact ;
– les forces à distance : les deux corps ne sont pas nécessairement au contact l’un de l’autre : forces de gravitation, forces électriques et forces électromagnétiques. Chacune de ces forces est répartie sur l’ensemble du corps, mais elles sont chacune modélisées par une force unique qui s’exerce toujours sur le centre de masse.
|
2. Systèmes matériels
particuliers
Un système isolé est un système qui n’est soumis à aucune force extérieure.
Un système pseudo-isolé est un système qui est soumis à des forces extérieures qui se compensent globalement :

|
3. Première loi
de Newton (ou principe de l’inertie)
Lorsqu’un solide est isolé ou pseudo-isolé, il existe toujours un point particulier G du solide, appelé centre d’inertie, qui peut :
– soit être au repos, s’il est initialement au repos 
– soit être animé d’un mouvement rectiligne uniforme : 
Que le système soit déformable ou indéformable, qu’il soit formé d’une ou de plusieurs parties, le centre d’inertie (C.I.) d’un système est toujours confondu avec le centre de masse (appelé aussi centre de gravité).
Ce principe n’est valable que dans certains référentiels appelés référentiels galiléens. La Terre (ou le laboratoire) peut être considérée comme un référentiel galiléen. Tout référentiel animé d’un mouvement rectiligne uniforme par rapport à un référentiel galiléen est aussi galiléen.
|
4. Troisième loi
de Newton : principe des actions réciproques
3. Exemples de forces
1. Le poids 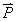 d’un corps
d’un corps
 |
La Terre exerce sur tout objet une force de pesanteur appelée
poids de l’objet, noté P. Ses caractéristiques
sont :
– direction : verticale
– sens : vers le bas
– valeur : P = mg
– point d’application : centre d’inertie de
l’objet.
g intensité de la pesanteur est fonction du lieu et de
l’altitude à la surface de la Terre ; en moyenne
g = 9,8 N.kg-1. |
2. La réaction
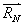 d’un support
sur un solide d’un support
sur un solide
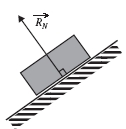 |
Cette
force de contact, répartie sur la surface de contact,
est exercée par un support sur l’objet.
Son point d’application est le centre de la surface de
contact (si la répartition est uniforme).
Sa direction est normale (orthogonale) à la surface de
contact ; son sens est vers le haut.
|
3. Forces de frottement

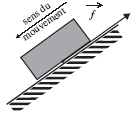 |
Ce sont des forces
réparties, exercées par tout corps en contact avec
le système étudié.
Leur point d’application est le centre de la surface de
contact (si la répartition est uniforme).
Leur direction est celle du déplacement, mais son sens
est inverse de celui du déplacement si le système
étudié est en mouvement.
Leur valeur dépend de la nature des surfaces en contact,
de la vitesse, de la forme du mobile...
Remarque : la réaction totale d’un support sur un
solide est :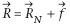 |
4. Force de rappel 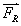 exercée par un ressort sur un solide
exercée par un ressort sur un solide
4. Deuxième loi
de Newton
1. Variations du vecteur
vitesse
Dans le cas où les forces extérieures appliquées à un système ne se compensent pas 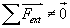 , alors le système voit son état de repos ou de mouvement modifié. , alors le système voit son état de repos ou de mouvement modifié.
Il y a une modification du vecteur vitesse de son centre d’inertie.
|
2. Vecteur accélération

|
L’accélération
représente le taux de variation de la vitesse par rapport
au temps, pour une durée  t
la plus petite possible. Le vecteur accélération
est égal à la dérivée première
du vecteur vitesse par rapport au temps. t
la plus petite possible. Le vecteur accélération
est égal à la dérivée première
du vecteur vitesse par rapport au temps.
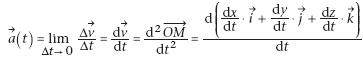
Le
repère étant fixe, les vecteurs unitaires , i
j k et sont des vecteurs constants dans le temps et par suite,
on a : 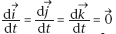
L’expression
du vecteur accélération est donc 
d’où
: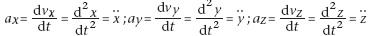
|
La valeur de l’accélération est :
Son unité dans le système international est le mètre par seconde au carré (m.s–2).
|

|
Ex
7 p.212
|
 |
Ex
8 p.212
Ex 20 p.215
|
3. Les différents
types de mouvements
|
|
 |
Ex
10 p.213
Ex 16/18
p.214 |
4. Deuxième loi
de Newton appliquée au centre d’inertie

|
Ex
14 p.213
|
 |
Ex
22 p.215 |
Objectif
bac p.217/218
|