1. Introduction
Il s'agit d’étudier
des mouvements simples à partir de films vidéos. En connaissant
la vitesse d’enregistrement du film (souvent 25 ou 30 images par
seconde) et en l'étudiant image par image, on peut connaître
la position d’un objet en fonction du temps. Pour cela nous allons
utiliser ici le logiciel Regressi et un logiciel de pointage. Ensuite
nous utiliserons un tableur pour modéliser les forces de frottements.
2. Exploitation du film
On vous propose d'utiliser
3 films de chutes de billes de diamètres et masses différentes
en mouvement dans un fluide constitué d'un mélange de
liquide vaisselle (85%) et d'eau (15%).
Film
1 : Chute d'une bille de 16 mm
Film 2 : Chute d'une bille
de 19 mm
Film 3 : Chute d'une bille
de 22 mm
1. Manipulation
Lancer Aviméca. Ouvrir le film 1. Faire l'étalonnage.
Il faut maintenant pointer de la façon la plus précise possible les positions successives du centre de la bille.
Faire ensuite Fichier>mesure>copier dans le presse-papier>tableau
Ouvrir regressi
Faire fichier>nouveau>presse papier. Une fenêtre contenant les données faites s'ouvre. On obtient la représentation de y en fonction de x.
|
2. Calcul de
la vitesse
Dans Regressi on obtient la représentation de y en fonction de x
Avec l'orientation des axes choisie, la vitesse de chute est l'opposé de la dérivée de y par rapport au temps.
Il faut opérer en deux étapes : calculer la dérivée puis changer le signe.
-
Calcul de la dérivée
Passer dans la fenêtre des grandeurs de Regressi
Choisir "Ajouter une grandeur".
Dans un premier temps on va calculer la dérivée de y par rapport au temps.
La nouvelle grandeur doit être de type "Dérivée".
La nommer, par exemple, "dery" et la définir comme dy/dt.
Cliquer sur OK.
- Calcul de la vitesse
On va maintenant calculer la vitesse. Pour cela il faut ajouter une autre grandeur.
Choisir cette fois une "Grandeur calculée", la nommer v et la définir comme l'opposé de la dérivée précédente.
Cliquer sur OK.
Passer dans l'onglet "Variables" pour observer le tableau
Il y a les valeurs des dates, de x, de y, de la dérivées de y par rapport au temps et celles de la vitesse.
|
3. Représentation
de la vitesse
Repasser dans la fenêtre "Graphique".Afficher la fenêtre des coordonnées.
Choisir maintenant de représenter la vitesse v en fonction du temps t avec une ligne de type "Lissage" d'ordre "3" et des points tracés par des "Croix".
Cliquer sur OK.
On obtient la courbe souhaitée.
Sur cette courbe on distingue bien le régime transitoire (vitesse croissante) et le régime permanent (vitesse constante).
Remarque : La vitesse initiale est rarement nulle car le début du mouvement n'est pas synchronisé avec la prise d'une image.
Estimer la valeur de la vitesse limite vlim.
Déterminer le temps caractéristique de la chute.
|
3. Modélisation
de la courbe
Théorie
Soit v(t) la vitesse mesurée à différents
instants t lors de la chute. La méthode d'euler donne v(ti+1)
= v(ti) +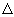 t
. v'(ti) t
. v'(ti)
L'équation différentielle qu'il faut résoudre
est 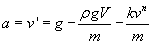
à t = 0 v0= 0 d'où

à t=1 v1 = v0+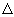 t
v'0 d'où v1 = t
v'0 d'où v1 = 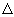 t
.( t
.( 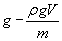 ) )
etc
|
=> Enregistrer vos données sous
NOM1
Recommencer pour les autres
vidéo ( Ne pas oublier d'enregistrer vos
données sous NOM2 et NOM3)
Que peut-on dire sur
la vitesse limite vlim des trois vidéos ?
Que peut-on dire sur le temps caractéristique de la chute des
trois vidéos ?
Conclure.
|