1. Mouvement plan d’un
projectile dans un champ de pesanteur uniforme
1. Équations horaires
paramétriques
Nous
reprenons l’étude du solide soumis à son seul
poids, mais avec une vitesse initiale non nulle. En se plaçant
dans un référentiel terrestre supposé galiléen,
d’après la deuxième loi de Newton, on a:
 soit
soit 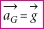
Choisissons
un repère orthonormé (O ;  ,
,  , ,  )
tel que la position initiale soit sur l’axe Oz et le vecteur
vitesse initial soit dans le plan vertical (O ; )
tel que la position initiale soit sur l’axe Oz et le vecteur
vitesse initial soit dans le plan vertical (O ;  ,
,  ). Nous considérons
les conditions initiales : ). Nous considérons
les conditions initiales :
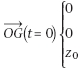 et
et 

|
Comme
les coordonnées de g sont : 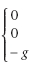 ,
on a : ,
on a : 
Par intégrations successives de l’accélération
et en tenant compte des conditions initiales, on a :
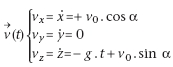 et
et 
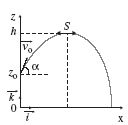
Quelle que soit la date t, on a y = 0 : la trajectoire est donc
décrite dans le plan (Ox, Oz).
|
2. Équation
de la trajectoire
|
D’après
(7), on a : 
En injectant cette relation dans (9), on en déduit l’équation
de la trajectoire :
 (10).
(10).
La
trajectoire est plane et parabolique. |
3. Flèche
de la trajectoire
La flèche
est l’altitude maximale h atteinte par le mobile, c’est-à-dire
l’ordonnée zS du sommet S. En ce point, la
tangente à la trajectoire et donc le vecteur vitesse sont horizontaux,
d’où :
 ,
soit ,
soit 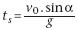
D’après (9), on a alors  , ,
soit 

|
Ex
6 p.252
Ex 17 p.255
|
 |
Ex
9/11 p.252
Ex 15/16/18
p.255
Ex 20 p.256 |
2. Le mouvement des planètes
: les trois lois de Képler
Le mouvement des planètes
s’étudie dans le repère héliocentrique dont
l’origine est le centre d’inertie du Soleil et dont les
trois axes sont dirigés vers trois « étoiles fixes
». Il est considéré comme galiléen.
1. Première loi
de Képler
Dans un
repère héliocentrique, les centres des planètes
décrivent des ellipses dont le centre du Soleil est l’un
des foyers.
La figure ci-dessous montre l’ellipse de foyers S (centre du
Soleil) et F2 décrite par le centre de la planète P.
2. Deuxième loi
de Képler (loi des aires)

|
Le rayon
Planète-Soleil « balaie » des aires proportionnelles
aux durées mises pour les « balayer ».
On remarque, que les aires A1, A2 et A3 sont « balayées
» par le rayon PS pendant la même durée : elles
sont donc égales.
On en déduit, intuitivement, que les arcs parcourus sont
tels que : l1 > l2 > l3.
La planète a donc sa plus grande vitesse, sur son orbite,
aux alentours du point A qui est le plus proche du Soleil ; au
contraire, la vitesse la plus faible est atteinte en A’,
point le plus éloigné du Soleil.
Si on assimile l’orbite planétaire à un cercle
de centre O, on en déduit que la planète se déplace
à vitesse constante : le mouvement est alors considéré comme circulaire uniforme. |
3. Troisième loi
de Képler
T étant
la période (temps nécessaire pour effectuer une révolution
sur l’orbite) et 2a = AA’ le grand axe, on écrit
:
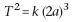 ou
ou 
Cette
constante k’ est la même pour toutes les planètes
du système solaire, ce qui a des applications importantes en
astronomie.
Pour deux planètes P et P’ du système solaire,
on peut écrire :
 soit soit

Cela permet
de déterminer la valeur de a’ et donc la trajectoire
de la planète P’.

|
Ex
13 p.253
|
 |
Ex
10 p.253 |
3. Le mouvement des satellites
1. Force de gravitation


|
Dans un repère
géocentrique supposé galiléen, un satellite
subit une force de gravitation de la part de la Terre :
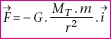 (12) (12)
où G = 6,67.10–11
S.I.
En assimilant la force de gravitation à une force de
pesanteur et le champ de gravitation au champ de pesanteur,
on a : 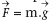 . .
On en déduit, d’après (12) :  (13). (13). |
2. Satellite à
trajectoire circulaire
 d'où
d'où  (14). Or, on démontre que
(14). Or, on démontre que  (15)
(15)
avec at,
accélération tangentielle et an, accélération
normale.
On en déduit que : 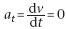 .
La valeur de la vitesse du satellite est donc constante : un satellite
à trajectoire circulaire a un mouvement uniforme. .
La valeur de la vitesse du satellite est donc constante : un satellite
à trajectoire circulaire a un mouvement uniforme.
Remarque : l’accélération étant radiale
centripète, on démontre que la trajectoire d’un
satellite est située dans un plan passant par le centre O de
la Terre.
3. Calcul de la vitesse
d’un satellite à trajectoire circulaire
Comme
an = g, on a 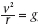 ,
d’où ,
d’où  .
Soit : .
Soit : 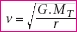
La vitesse du satellite n’est fonction que de sa distance au
centre de la Terre, c’est-à-dire de son altitude.
4. Calcul de la période
de révolution d’un satellite à trajectoire circulaire
La période
de révolution correspond à la durée d’un
tour, soit :
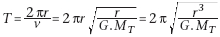 .
On en déduit : .
On en déduit :
Le rapport  est donc constant et indépendant de la masse du satellite :
il ne dépend que de la masse responsable de l’attraction
gravitationnelle (3e loi de Képler).
est donc constant et indépendant de la masse du satellite :
il ne dépend que de la masse responsable de l’attraction
gravitationnelle (3e loi de Képler).
Dans le
référentiel géocentrique, la vitese et la période
d'un satellite animé d'un mouvement circulaire et uniforme
autour du centre de la Terre dépendent uniquement de l'altitude
du satellite. Quand l'altitude augmente, la vitesse diminue et la
période augmente.
Remarque
: Il existe des satellites dits géostationnaires. Ils parcourent
dans le référentiel géocentrique un cercle équatorial
à une altitude voisine de 36 000 km, décrit d'Ouest
en Est avec une vitesse angulaire de révolution égale
à celle de la rotation de la Terre autour de l'axe des pôles
T=86 164 s.
Objectif
bac p.258/259/260
|
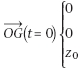 et
et 

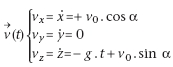 et
et 





 d'où
d'où  (15)
(15)