1. Notion d’oscillateur
mécanique
1. Définition
On appelle oscillateur
(ou système oscillant) un système pouvant évoluer,
du fait de ses caractéristiques propres, de façon périodique
et alternative autour d’une position d’équilibre
(ex : suspension de voiture, balançoire...).
2. Caractérisation
des oscillateurs mécaniques
La grandeur
oscillante intervenant dans les équations est ici l’écart
à l’équilibre. C’est une grandeur algébrique.
Cet écart est en général repéré
:
– soit par l’abscisse rectiligne x(t) dans le cas d’une
oscillation rectiligne (système solide-ressort) ;
– soit par l’abscisse angulaire 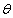 (t)
dans le cas d’une oscillation circulaire (système pendulaire). (t)
dans le cas d’une oscillation circulaire (système pendulaire).
La valeur positive extrême (ou maximale) prise par x(t) et 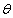 (t)
définit l’amplitude de l’oscillation. (t)
définit l’amplitude de l’oscillation.
3. Le pendule
simple
Un pendule
simple est un oscillateur élémentaire. C’est un
modèle idéalisé du pendule pesant dans lequel
la masse suspendue peut être considérée comme
ponctuelle.

Lorsqu’on
écarte un pendule pesant ou un pendule simple de sa position
d’équilibre d’une abscisse angulaire 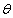 0
et qu’on l’abandonne à lui-même, on constate
que, pour des valeurs de 0
et qu’on l’abandonne à lui-même, on constate
que, pour des valeurs de 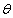 0
n’excédant pas une dizaine de degrés, celui-ci
effectue des oscillations libres dont la période T est indépendante
de 0
n’excédant pas une dizaine de degrés, celui-ci
effectue des oscillations libres dont la période T est indépendante
de 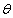 0.
On dit que le pendule simple et le pendule pesant vérifient
la loi d’isochronisme des petites oscillations. 0.
On dit que le pendule simple et le pendule pesant vérifient
la loi d’isochronisme des petites oscillations.
Selon l’importance des frottements de l’amortissement,
il y a plusieurs régimes libres possibles une fois que le pendule
est abandonné à lui-même :


|
Dans le cas du pendule
simple sans frottement, la période des oscillations T0
est appelée période propre. L’expérience
montre qu’elle ne dépend que de la masse du pendule
et de la longueur du fil : 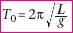 , ,
où L est la longueur du fil (en mètre) et g est
l’intensité de pesanteur. |
Avec
frottements, la période T de l’oscillation est inférieure
à T0. Mais si l’amortissement est faible, on peut considérer
que T ˜ T0.
4. Position
d'équilibre
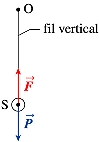
|
A
l'équilibre, le fil qui supporte le solide S est vertical.
Cette position d'équilibre est stable. Ecarté
de la verticale et lâché sans vitesse, un pendule
simple oscille de part et d'autre de sa position d'équilibre.
Son mouvement est plan. |

|
Ex
7/8 p.274
Ex 11/12/14
p.275
Ex 18 p.276 |
 |
Ex
16/17 p.276
Ex 19 p.277 |
Objectif bac p.279/280
2. Le pendule élastique
1. Dispositif expérimental
Un solide (S) de masse
m pouvant coulisser sur un rail horizontal est fixé à
l’extrémité d’un ressort de masse négligeable
à spires non jointives. L’autre extrémité
du ressort est accrochée à un point fixe.
On repère la position de (S) par l’abscisse x(t) de son
centre de gravité, choisie nulle lorsque le système
est au repos. Ainsi x(t) est directement l’écart à
l’équilibre.
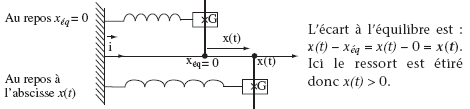
Le bilan
des forces extérieures appliquées au système
(S) dans le référentiel terrestre supposé galiléen
après l’avoir écarté de sa position d’équilibre
de x0 puis lâché sans vitesse initiale est :
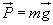 ,
le poids de (S) ; ,
le poids de (S) ; 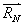 ,
la réaction normale du rail supportant (S) ; ,
la réaction normale du rail supportant (S) ;  ,
la force équivalente réunissant les forces de frottement
avec le rail et avec l’air ; et la force de rappel du ressort ,
la force équivalente réunissant les forces de frottement
avec le rail et avec l’air ; et la force de rappel du ressort
La résultante
des forces est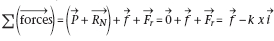

|
Ex
9 p.294
Ex 11 p.295
|
 |
Ex
10 p.295 |
2. Équation différentielle
Appliquons le théorème
du centre d’inertie au système (S) dans le référentiel
terrestre supposé galiléen :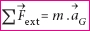 (1).
(1).
Ces forces étant colinéaires, on projette (1) selon
l’axe Ox uniquement. On obtient : 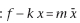 ,
soit : ,
soit : 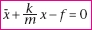 (2). (2).
De même que pour le pendule simple et selon l’intensité
des frottements,on peut envisager plusieurs régimes libres
: régime apériodique, régime critique, régime
pseudo-périodique, régime périodique. On vérifie
également l’isochronisme des petites oscillations.
3.Solution analytique
de l’équation différentielle pour f = 0
Dans le
cas où les frottements sont négligeables, l’équation
(2) se réduit à 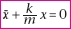 (3) : c’est une équation différentielle du second
ordre.
(3) : c’est une équation différentielle du second
ordre.
La solution de cette équation est l’équation horaire
d’un mouvement libre non amorti. Elle est de la forme : 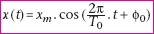 (4), (4),
où 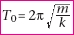 est la période propre de l’oscillateur, où xm
est l’amplitude de l’oscillation et où
est la période propre de l’oscillateur, où xm
est l’amplitude de l’oscillation et où 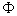 0
la phase à l’origine des dates (déterminables
par les conditions initiales). 0
la phase à l’origine des dates (déterminables
par les conditions initiales).
La condition initiale v(0) = 0 impose ici 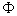 0
= 0 radian. 0
= 0 radian.
La condition initiale x(0) = x0 impose ici xm = x0.


|
Ex
15 p.296
|
 |
Ex
17 p.296
Ex 21 p.297 |
3. Le phénomène
de résonance
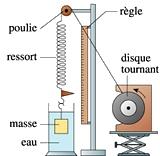
1. Excitation d’un
système « solide-ressort »
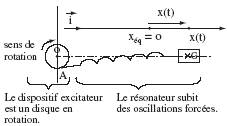
|
Considérons
à nouveau le dispositif de la partie 2 en accrochant
cette
fois le point A du ressort à la périphérie
d’un disque dont la fréquence de rotation est
contrôlable.
Ceci constitue un dispositif d’excitation.
Le mouvement de G n’est plus libre : on parle d’oscillations
forcées.
On s’arrange en général pour que OA soit
négligeable devant AG afin de pouvoir considérer,
dans l’étude, que le ressort reste horizontal.
Ainsi, le disque tournant à la fréquence N (période
T) impose un mouvement horizontal de G à la même
fréquence (et donc de même période T).
L'amplitude xm du mouvement du résonateur dépend,
pour un amortissement donné, de la période imposée
par l'excitateur.
|
2. Excitation d’un
pendule simple
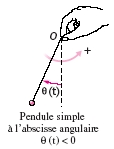
|
Considérons
à nouveau le pendule simple de la partie 1. Il est tenu
cette fois en O par un opérateur pouvant imposer un petit
mouvement de balancier de période T au pendule.
Dans cette situation, on dit que le pendule est excité.
C’est l’opérateur qui constitue l’excitateur.
|
3. Résonance
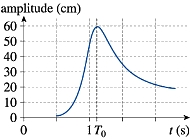
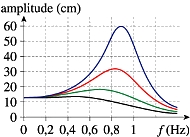
Influence de l'amortissement |
Dans
le cas « solide-ressort » comme dans celui du pendule
simple, le dispositif excité reproduit un mouvement plus
ou moins amplifié de l’excitateur en fonction de
la fréquence d’excitation.
Lorsqu’il n’y a pas de frottements, le mouvement
de (S) est le plus ample pour une période d’excitation
égale à la période propre du système.
On dit alors qu’il y a résonance.
Sans
frottement, il y a résonance pour T = T0.
Avec des frottements faibles, la résonance a lieu pour
T ˜ T0. |
Si les
frottements sont faibles, l’amplitude à la résonance
est importante mais uniquement pour des excitations de période
T très proches de T0 : on parle de résonance aiguë.
Exemple : un microphone très sensible à une zone étroite
de fréquence de son constitue un résonateur à
résonance aiguë ; un micro de chanteur par exemple est
relativement sélectif.
Si au contraire l’amortissement est fort, l’amplitude
à la résonance n’est pas très grande. La
résonance s’observe aussi pour des excitations dont les
périodes T font partie d’un voisinage plus large de T0
: on parle de résonance floue.
Exemple : un haut-parleur de chaîne Hi-Fi doit être capable
de restituer des sons de fréquences diverses ; il constitue
un résonateur à résonance floue.

|
Ex
16 p.296
Ex 22 p.297
|
|
|
Objectif
bac p.299/300
|