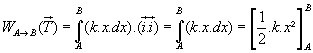1. Travail d’une
force
1. Introduction
On sait qu’une force
appliquée à un système (S) est capable de modifier
son mouvement (direction, sens et/ou valeur de la vitesse). Une force
est donc capable d’augmenter ou de diminuer l’énergie
cinétique de (S) dont l’expression est : Ec=1/2 mvG²
pour un solide en translation de centre de gravité G.
On peut donc considérer qu’une force est un convertisseur
d’énergie. Elle permet de convertir une forme d’énergie
en une autre, l’une des deux étant sous forme d’énergie
cinétique et l’autre dépendant de la nature de
la force.
La quantité d’énergie que la force convertit en
énergie cinétique est appelée travail de la force,
noté W( )
et s’exprimant en joule (J). C’est une grandeur algébrique,
son signe indique le sens du transfert de l’énergie : )
et s’exprimant en joule (J). C’est une grandeur algébrique,
son signe indique le sens du transfert de l’énergie :
– si W( )
> 0, l’énergie cinétique du système
augmente : on dit que la force est motrice ; )
> 0, l’énergie cinétique du système
augmente : on dit que la force est motrice ;
– si W( )
< 0, son énergie cinétique diminue, la force est
résistante. )
< 0, son énergie cinétique diminue, la force est
résistante.
2. Travail
élémentaire
En classe
de première, pour une force constante en direction, sens et
valeur sur un déplacement rectiligne MM', on définit
le travail de cette force par la relation : WM->M'( )
= )
=  . . 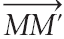 . .
3. Travail
total
Pour trouver
le travail total de A à B, on fait la somme de tous les travaux
élémentaires. Comme il y a une infinité de déplacements
élémentaires pour aller de A à B, la somme de
ces travaux n’est pas une somme discrète (  ) mais une somme continue : il s’agit d’une somme au sens
) mais une somme continue : il s’agit d’une somme au sens
intégrale ( ).
).
4. Travail
d’une action sur un ressort

|
Ex
8 p.313
|
|
|
2. Énergie mécanique
d’un système « solide-ressort » horizontal
1. Énergie potentielle
élastique d’un ressort seul
La tension  exercée par un opérateur qui comprime ou qui étire
un ressort à partir de sa position de repos est une force qui
convertit l’énergie cinétique fournie par l’opérateur
en énergie potentielle élastique (pour le ressort).
exercée par un opérateur qui comprime ou qui étire
un ressort à partir de sa position de repos est une force qui
convertit l’énergie cinétique fournie par l’opérateur
en énergie potentielle élastique (pour le ressort).
Bien que l’énergie cinétique diminue, le travail
de  est positif
; il s’agit en effet de l’énergie cinétique
possédée par l’opérateur et non celle du
système constitué par le ressort. est positif
; il s’agit en effet de l’énergie cinétique
possédée par l’opérateur et non celle du
système constitué par le ressort.
On a :  EP
A->B = WA->B ( EP
A->B = WA->B ( ) , soit : EPB–EPA : ½.k(xB²
- xA²) = ½.kxB²- ½.kxA²
) , soit : EPB–EPA : ½.k(xB²
- xA²) = ½.kxB²- ½.kxA²

2. Étude énergétique
du système « solide-ressort »
Remarque :  est une force intérieure au système. D’habitude,
le bilan des forces ne fait intervenir que des forces exercées
par le milieu extérieur car les systèmes étant
en général indéformables, les forces intérieures
ne travaillent pas.
est une force intérieure au système. D’habitude,
le bilan des forces ne fait intervenir que des forces exercées
par le milieu extérieur car les systèmes étant
en général indéformables, les forces intérieures
ne travaillent pas.
Ici, le système étant déformable, cette force
travaille. Elle convertit de l’énergie cinétique
possédée par la masse en énergie potentielle
élastique communiquée au ressort).
On applique le théorème
de l’énergie cinétique sur le premier quart de
période du mouvement (G passe de Gm à O). Seule,  travaille sur une distance valant GmO.
travaille sur une distance valant GmO.

On obtient
 Ec Gm->O
= Ec Gm->O
=  EP Gm->O,
soit : EP Gm->O,
soit :  Ec
Gm->O = Ec
Gm->O =  EP
Gm->O = 0. EP
Gm->O = 0.
En introduisant l’expression de l’énergie mécanique
Em = EP + Ec, on peut écrire  Em
= 0. L’énergie mécanique du système se
conserve : le système est dit conservatif. Em
= 0. L’énergie mécanique du système se
conserve : le système est dit conservatif.

|
Sur
ce premier quart de période, toute l’énergie
potentielle initiale du ressort est convertie en énergie
cinétique pour la masse par la force F.
La masse atteint sa vitesse maximale en O, mais le ressort ne
possède plus d’énergie potentielle. |
Puis
G passe de O à Gm’ tel que x = – xm (deuxième
quart de période),  change alors de sens et convertit alors l’énergie cinétique
en énergie potentielle... Il y a transfert mutuel d’énergie
cinétique en énergie potentielle élastique au
cours de ce mouvement périodique.
change alors de sens et convertit alors l’énergie cinétique
en énergie potentielle... Il y a transfert mutuel d’énergie
cinétique en énergie potentielle élastique au
cours de ce mouvement périodique.

|
Ex
9/10 p.314
|
 |
Ex
11 p.314
Ex 15/16
p.315
Ex 18/19
p.316 |
3. Énergie d’un
projectile dans un champ de pesanteur uniforme
1. Travail du poids

|
La force gravitationnelle
exercée par la terre sur un objet de son voisinage
est appelée le « poids de l’objet »
: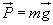 ,
où ,
où  est le vecteur champ de pesanteur. Si les distances parcourues
à la surface de la Terre ne dépassent pas quelques
kilomètres,
est le vecteur champ de pesanteur. Si les distances parcourues
à la surface de la Terre ne dépassent pas quelques
kilomètres,  peut être considéré comme constant : on
dit que le champ de pesanteur est uniforme.
peut être considéré comme constant : on
dit que le champ de pesanteur est uniforme.
Lorsque l’objet change d’altitude, son poids travaille.
Il convertit alors de l’énergie cinétique
en énergie potentielle de pesanteur ou inversement
selon qu’il gagne ou perd de l’altitude :
– si l’objet perd de l’altitude, W(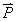 )
> 0 : on dit que )
> 0 : on dit que 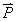 est moteur,
est moteur,
– si l’objet monte, W(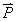 )<
0 : on dit que )<
0 : on dit que 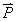 est résistant.
est résistant.
Lors d’un déplacement élémentaire
 , le
travail élémentaire du poids est : , le
travail élémentaire du poids est :
dW(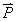 )
= )
= 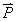 . . = m.g.(
= m.g.( . . )
= m.g.dz. )
= m.g.dz.
De A à B, si  est constant, on a :
est constant, on a :


Dans
l’exemple, on a : zB < zA, donc WA->B(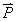 ) > 0.
) > 0.
Ce travail est indépendant du chemin suivi entre A
et B, il ne dépend que des altitudes de départ
et d’arrivée.
|
2. Énergie potentielle
de pesanteur
WA->B(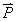 ) = – mg.(zB – zA) = – (mg.zB
– mg.zA ) = – (EPB – EPA)
= –
) = – mg.(zB – zA) = – (mg.zB
– mg.zA ) = – (EPB – EPA)
= –  EP
A->B. EP
A->B.
L’énergie potentielle de pesanteur est donc :  ,
si on la considère comme étant nulle à l’altitude
z = 0. ,
si on la considère comme étant nulle à l’altitude
z = 0.
3. Énergie mécanique

|
Ex
13 p.314
|
 |
Ex
14/17 p.315 |
Objectif bac p.318/319/320
|