 |
La
numération au cours des temps |
 |
Vous devez répondre
individuellement par écrit aux questions
posées (si possible réaliser le compte rendu sur
traitement de texte), sachant que les réponses à
ces questions sont présentes dans ce site Internet ; mais,
bien évidemment vous notez – en plus – toutes
les informations qui vous semblent utiles : vous
vous constituez votre propre cours. |
Objectifs
généraux :
- Etude des systèmes de numérisation à
travers les siècles
- Durée :1 séance
|
Matériel :
|
| I Les babyloniens |
Chez les Babyloniens ( environ 2000 ans av.J.C.
), les symboles utilisés sont le clou pour l’unité et le
chevron pour les dizaines. Le système est additif jusqu’à
60.
Clou 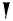 Chevron
Chevron 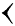

Cette numération est dite de position, car le nombre dépend de
la position des symboles utilisés
A partir de 60, la position des symboles entre en jeu de la façon
suivante :
| 204 |
7392 |
| 3
x 60 + 24 |
2
x 60² + 3 x 60 + 12 |
| 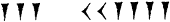
|
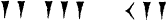
|
Comment comptaient-ils sur leurs doigts ?
Le pouce d’une main comptait les phalanges des quatre autres
doigts ( soit un maximum de 12 ) ;
une fois le maximum atteint, un doigt de l’autre main « retenait »
ce 12, si bien qu’au total avec les deux mains, cela fait 5 x12
= 60. |
| Q 1 : Écrire 182, 342 et 2001
en numération babylonienne : rédiger les solutions sur le compte-rendu. |
|
| II Les égyptiens |
 Les scribes égyptiens (environ 1800 av.
J.C.) représentaient 1 et les multiples de 10 par un croquis :
ci-contre les représentations des nombres fractionnaires. Les scribes égyptiens (environ 1800 av.
J.C.) représentaient 1 et les multiples de 10 par un croquis :
ci-contre les représentations des nombres fractionnaires.
| 1 |
10 |
100 |
1
000 |
10
000 |
100
000 |
1
000 000 |
| 
|
|
|
|

|
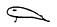
|
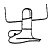
|
| |
|
Corde
enroulée |
Fleur
de lotus |
Doigt
coupé |
têtard |
Dieu
assis |
Pour lire un nombre, on additionne la valeur de l’ensemble des
symboles utilisés dans son écriture :
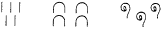 signifie 5 + 40 + 300 = 345
signifie 5 + 40 + 300 = 345
|
Q 2: Cette numération est-elle
une numération de position ?
Q 3 : Écrire 210, puis 3,5, puis 7,125 et enfin 2001 en numération
égyptienne : rédiger sur le compte rendu |
|
| III Les Mayas |
 La
civilisation maya s’étend vraisemblablement de 1500 av JC à nos
jours avec une apogée vers l’an 800 de notre ère. Les signes de
l’arithmétique et du calendrier (aussi précis que notre calendrier
actuel) ont été assez vite connus. Mais le sens de la plupart
des textes nous échappe encore, et on ne parvient pas à trouver
la clé qui permettrait de les traduire. La
civilisation maya s’étend vraisemblablement de 1500 av JC à nos
jours avec une apogée vers l’an 800 de notre ère. Les signes de
l’arithmétique et du calendrier (aussi précis que notre calendrier
actuel) ont été assez vite connus. Mais le sens de la plupart
des textes nous échappe encore, et on ne parvient pas à trouver
la clé qui permettrait de les traduire.
Les
chiffres (glyphes) représentent des têtes de divinités vues de
profil. Il y en a vingt : de zéro à dix-neuf. Les Maya avaient
en effet adopté une numération vigésimale, dans laquelle les unités
vont en croissant ou en décroissant de vingt en vingt : ils s'étaient
rendus compte qu'en se penchant un petit peu, ils pouvaient compter
aussi sur leurs orteils, d’où l’adoption de la base vingt.
Pour les calculs,
ils n’utilisent pas les glyphes, mais des signes très simples
:
-
le point qui vaut un,
-
le tiret qui vaut cinq
-
une sorte d’ovale figurant la coupe d’un coquillage
qui vaut zéro.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 
|
 
|
  
|
   
|
— |

— |
 
— |
  
—— |
   
–—— |
—
— |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
| 
—
— |
 
—
— |
  
——
—— |
   
–——
–—— |
—
—
— |

—
—
— |
 
—
—
— |
  
——
——
—— |
   
–——
–——
–—— |
|
Les chiffres de un à quatre s’écrivent
avec un à quatre points, de six à neuf avec un tiret surmonté
de un à quatre points, dix avec deux tirets l’un au-dessus de
l’autre, et ainsi de suite jusqu’à dix-neuf avec trois tirets
surmontés de quatre points.
Vingt est une unité du deuxième ordre,
soit un point placé en deuxième position. Car le système vigésimal
maya est une numération de position, comme notre système décimal,
mais au lieu de placer les unités à droite, les dizaines à gauche
des unités, etc., les Maya plaçaient les vingtaines au-dessus
des unités, les vingtaines de vingtaines au-dessus des vingtaines,
etc.
Prenons par exemple, le nombre 643 :
| Vingtaine
de vingtaines : 20 ´ 20 = 20² |

|
1
x 20² |
400 |
| Vingtaines :
20 = 201 |
 
–—
—– |
12
x 201 |
240 |
| Unités :
1 = 200 |
  
|
3
x
200 |
3 |
| |
|
Total |
643 |
La civilisation Aztèque éphémère
(1168, émergence de cette tribu – 1520, arrivée de Cortes le conquistadore
) utilisa aussi la numération de base 20, mais moins élaborée :
un point pour une unité, un fanion pour 20, trois fanions pour
60, une branche pour 400. |
| Q 4 : Écrire les nombres 264 et
2001 en « maya » |
|
| IV Les
chinois |
 Depuis 500 ans av. J.C., les Chinois ont
inventé la première calculatrice dont ils se servent encore de
nos jours (les jeunes élèves apprennent toujours à l’école à compter
avec le boulier) avec une efficacité remarquable. Il repose sur
les dix doigts de la main et sur les positions des chiffres dans
le nombre. Depuis 500 ans av. J.C., les Chinois ont
inventé la première calculatrice dont ils se servent encore de
nos jours (les jeunes élèves apprennent toujours à l’école à compter
avec le boulier) avec une efficacité remarquable. Il repose sur
les dix doigts de la main et sur les positions des chiffres dans
le nombre.
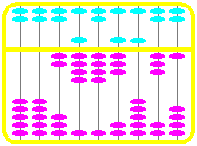
Le boulier de 11 tiges ci-contre permet une capacité de calcul
de 1011 –1 unités. Attention, il est représenté ci-contre
en cours de calcul (une multiplication) et le nombre final n’a
pas encore un affichage optimisé.
|
| Q 5 : Exprimer le
plus petit et le plus grand nombre accessible. |
Un boulier « se lit » de droite à gauche,
la première colonne représentant les unités, la seconde les dizaines,
la troisième des centaines, etc. (Certains attribuent aux deux premières :
1/100 et 1/10 )
La ligne du haut comporte deux boules qui valent chacune 5 unités,
La ligne du bas comprend 5 boules valant chacune une unité.
Les boules sont « actives » si elles sont en bas sur
la ligne du haut et en haut sur la ligne du bas, donc
la lecture est faite le long de la barre de séparation.
Le boulier (1) indique le nombre 2 948 531 soit (0+0) ;(0+0) ;(0+2) ;(5+4) ;(0+4) ;(5+3) ;(5+0) ;(0+3) ;(0+1)
|
(1) |
| Q 6 : Quel nombre indique le
boulier ? |
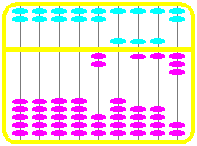
(2) |
Pour faire une addition, on effectue l’addition colonne par colonne
en tenant compte des retenues dans la colonnes suivantes :
Q 7 : trouvez la somme des deux nombres précédents (1) + (2) et
l’inscrire dans la case (3). |

(3) |
|
| V La numération
binaire |
Dans la vie courante, nous pratiquons
la numération décimale …reposant à l’origine sur nos dix doigts :
les dix symboles – chiffres – permettent de représenter tous les
nombres.
La position
des chiffres est primordiale dans cette représentation (numération
de position) : il y a quelques années déjà, vous avez appris ce
qu’étaient les unités (colonne de droite), les dizaines, les centaines,
etc.
Ainsi on peut écrire
4138
comme 4 x 1000 + 1 x 100 + 3 x 10 + 8 x 1
On remarque les égalités
suivantes :
1000 = 103 ; 100 = 10² ; 10 = 101 ;
1 = 100
Donc 4138 peut s’écrire :
4 x 103 + 1 x 102 + 3 x 101 +
8 x 100
où 10 est appelé BASE de cette numération (ici décimale),
où chaque chiffre (compris entre 0 et 9) est soit celui des unités,
dizaines, etc
On peut généraliser
cette définition à une numération à base n :
-
Si n = 2 alors on
a le binaire : tout nombre est écrit avec 0 et 1
-
Si n = 16 alors on
a l’hexadécimal : tout nombre s’écrit grâce à 0, 1, 2,
3, 4, 5, 6 ,7, 8, 9, A, B, C, D, E, et F
-
Si n = 20 on a le
vigésimal (cf. les mayas)
|
Un exemple plus récent : le bibinaire   Boby
LAPOINTE, chanteur, acteur et humoriste replonge, en 1968, (quelques
temps plus tôt il avait eu un bac Math Elem , term S maintenant !)
dans les mathématiques et met au point le système bi-binaire,
qui lui vaudra un succès d'estime auprès de la communauté scientifique
en 1971. Boby
LAPOINTE, chanteur, acteur et humoriste replonge, en 1968, (quelques
temps plus tôt il avait eu un bac Math Elem , term S maintenant !)
dans les mathématiques et met au point le système bi-binaire,
qui lui vaudra un succès d'estime auprès de la communauté scientifique
en 1971.
A cette époque, le binaire était utilisé (deux
« chiffres » 0 et 1), ainsi que l’hexadécimal (16 « chiffres »
de 0 à 9 puis A, B, C, D, E, F).
Rappelons que B. Lapointe était originaire du
sud de la France … pays de la bibine ou vin de mauvaise qualité,
encore un trait d’humour de sa part !
Considérons les quinze premiers nombres naturels (de 0 à 15)
écrits en base deux et complétés par des zéros à gauche. Cela
donne le tableau suivant pour ces nombres :
| Décimal |
|
Décimal |
|
Décimal |
|
Décimal |
|
| 0 |
00
00 |
4 |
01
00 |
8 |
10
00 |
12 |
11
00 |
| 1 |
00
01 |
5 |
01
01 |
9 |
10
01 |
13 |
11
01 |
| 2 |
00
10 |
6 |
01
10 |
10 |
10
10 |
14 |
11
10 |
| 3 |
00
11 |
7 |
01
11 |
11 |
10
11 |
15 |
11
11 |
Boby LAPOINTE
remarqua que tous les nombres pouvaient être découpés en tranches,
chacune des tranches pouvant être 00, 01, 10 ou 11.
Pour les groupes de droite,
il choisit des voyelles : 00 = o ; 01 = a ; 10 = e ; 11 = i
Pour les groupes de gauche,
il fit le choix de consonnes : 00 = H ; 01 =
B ; 10 = K ; 11 = D
Donc compter de 0 à 15 donne
cette « comptine » :
Ho,
Ha, He, Hi, Bo, Ba, Be, Bi, Ko, Ka, Ke, Ki, Do, Da, De, Di
Pour écrire un nombre, il suffit
de combiner ces phonèmes :
17 = 1 x 16 + 1 : HaHa 1997 = 7 x 16² + 12 x
16 + 13 : BiDoDa |
Q 8 : Cette
numération est-elle une numération de position ?
Q 9 : Que vaut le nombre bibinaire
"KeKiDiBiBi" en décimal ?
Q 10 : Ecrire 680 et 2001 en
numération bibinaire. |
|
VI Codage des informations
en informatique |
Les deux types de grandeurs
Les deux types de grandeurs susceptibles d’être codées sont :
- Les grandeurs analogiques : elles peuvent varier de manière
continue vers une autre valeur sans discontinuité.
- Les grandeurs numériques ou digitales ou discrètes qui évoluent
par saut c’est à dire par discontinuité.
|
Le codage binaire
C’est une grandeur numérique ne pouvant avoir que deux « valeurs » :
0 ou 1 ( donc de base …. )
| |
Interrupteur fermé
Le courant passe |

|
Interrupteur ouvert
Le courant ne passe pas |

|
| Attribution
à cet état |
de
la valeur : |
1 |
de
la valeur : |
0 |
L’état de cette grandeur BINAIRE est codé « sur
un » BIT ( Binary Digit ) soit 2 possibilités :
0 ou 1
| Nbre
d’interrupteurs |
Nbre
de caractères codables |
Ces
caractères |
Nbre
de BIT |
| 1 |
2 |
0,
1 |
1 |
| 2 |
4 |
00,
01, 10, 11 |
2 |
| 3 |
8 |
000,
001, 010, 011, 100, 101, 110, 111 |
3 |
| 4 |
16 |
0000,
0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001,
1010, 1011, 1100, 1101, 1110, 1111 |
4 |
| 8 |
32 |
00000,
00001, 00010, 00011, 00100, 00101, 00110, 00111, 01000,
01001, 01010, 01011, etc... |
5 |
Un mot de 8 bits s’appelle un octet et
représente 32 caractères codables ou possibilités.
| |
0
1 1 0 1 1 0 1 |
|
|
Le bit le plus à gauche est le bit de POIDS le plus fort |
|
Le bit le plus à droite est le bit de POIDS le plus faible |
| 
|
|

|
| |
Comparaison |
|
| |
4
1 3 8 |
|
| poids
fort = milliers |
|
poids
faible = unités |
|
Les capacités en informatique
Pour évaluer les capacités de stockage de données – donc de caractères
– on utilise l’octet comme unité et surtout ses multiples :
Q 11 : Compléter
Le kilo-octet ( Ko ) : 1 Ko = 210
octets = ……………… octets
Le méga-octet ( Mo ) :
1 Mo = 220 octets = ……………… octets
Le giga-octet ( Go ) : 1
Go = 230 octets = ……………… octets
Rappel historique : le
premier ordinateur familial (ZX Sinclair) avait 1 Ko de RAM
Les disquettes 5 ¼ pouces
stockaient 360 Ko puis 720 Ko.
Les disquettes 3 ½ pouces
stockent 720 ko puis 1,44 Mo
Les disquettes ZIP stockent
100 Mo puis 250 Mo, tandis que les bandes atteignent 50 Go et
les CD Rom 650 Mo |
|
| VII Les techniques
de codage |
|  Il a fallu assez tôt inventer des techniques
de codage quand Blaise Pascal inventa la première machine
à calculer (la « pascaline ») – il est vrai peu performante
et utilisant des engrenages. La première calculatrice digne de
ce nom (addition, soustraction, multiplication et même division)
fut mise au point par Leibniz (1646 – 1716) célèbre philosophe
et mathématicien allemand. Tout en nous familiarisant avec le maniement de
la base deux (écriture des nombres, pratique des opérations),
Leibniz au tout début du XVIII siècle nous en montre les avantages : Il a fallu assez tôt inventer des techniques
de codage quand Blaise Pascal inventa la première machine
à calculer (la « pascaline ») – il est vrai peu performante
et utilisant des engrenages. La première calculatrice digne de
ce nom (addition, soustraction, multiplication et même division)
fut mise au point par Leibniz (1646 – 1716) célèbre philosophe
et mathématicien allemand. Tout en nous familiarisant avec le maniement de
la base deux (écriture des nombres, pratique des opérations),
Leibniz au tout début du XVIII siècle nous en montre les avantages :
"Le
calcul ordinaire d'arithmétique se fait suivant la progression
de dix en dix. On se sert de dix caractères, qui sont 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, qui signifient zéro, un et les
nombres suivants jusqu'à neuf inclusivement. Et puis allant
à dix, on recommence, et on écrit dix par 10, et dix fois
dix ou cent par 100, et dix fois cent ou Mille par 1 000,
et dix fois mille par 10 000, etc.
Mais au lieu de la progression
de dix en dix j'ai employé depuis plusieurs années la progression
la plus simple de toutes, qui va de deux en deux, ayant
trouvé qu'elle sert à la perfection de la science des nombres.
Ainsi je n'y emploie point d'autres caractères que 0 et
1, et puis allant à deux, je recommence. C'est pourquoi
deux s'écrit ici par 10, et deux fois deux ou quatre par
100, et deux fois quatre ou huit par 1 000, et deux fois
huit ou seize par 10 000, et ainsi de suite. Voici la table
des nombres de cette façon, qu'on peut continuer tant que
l'on voudra." |

|
Q 12 : Continuez la table de
Leibniz jusqu’à 25.
Q 13 : Par quel chiffre se terminent les nombres pairs, les nombres
impairs écrits en base 2 ?
Q 14 : Que constatez-vous quand on passe, en base 2, de l’écriture
de 0 à 2, à 4, à 8, à 16, … ? |
Un autre codage
En informatique, les données sont également codées
en hexadécimal utilisant les 10 chiffres habituels auxquels on
ajoute les 6 premières lettres de l’alphabet en majuscules :
Donc 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A ->
10, B -> 11,
C ->12, D ->
13, E ->14,
F ->15. La base
utilisée est donc 16 : la méthode est donc similaire au décimal
en remplaçant 10 par 16.
Exemple : FAC = Fx162
+ Ax161 +
Cx160 = 15x162
+ 10x161 +
12x160 = 4012
Voici
pourquoi l'hexadécimal a été choisi : un processeur n’utilise
seulement que des 0 et des 1 ( binaire ). Mais c'est lourd à traduire :
1000 en hexadécimal -> 1 000 000 000 000 en binaire.
On a choisi une écriture
plus condensée : il s'agit de grouper les quartets ( donc
des blocs de 4 symboles consécutifs ) du code binaire 4 par 4.
Exemple : le décimal 125 est en fait codé en mémoire
par l’octet 01111101 (vérifier
cette valeur)
Séparons-le en 2 quartets : 0111 – 1101. Chaque quartet binaire
représente un nombre décimal : 7 – 13 (voir tableau Bibinaire),
ce qui donne 7D en hexadécimal
Application pratique 1 : la couleur « vert d’eau »
sur un moniteur est codée en hexadécimal 82DAB7
soit 8-2-13-10-11-7 ( tableau Bibinaire) c’est à dire 1000-0010-1101-1010-1011-0111
donc en binaire 100000101101101010110111 en mémoire, ce qui
correspond au décimal 8 575 671
Application pratique 2 : |
| Q 15 : Le noir est codé FFFFFF,
ce qui correspond à quel binaire ? à quel décimal ? Justifier
l’appellation 16 millions de couleurs pour nos « micros »
actuels. |
|
|
VIII Exercice Codages n°1 |
Voici des informations,
telles que l'on pourrait les voir à l'intérieur de la mémoire
d'un ordinateur :
| 001111000010101000100011011000110110010101100011
|
| 011010010010000100101000011001010111001101110100
|
| 001010010010011001110101011011100011111100101011
|
| 011011010110010101110011011100110110000101100111
|
| 011001010010000100101101011100110111010101100010
|
| 011011000110100101101101011010010110111001100001
|
| 01101100001000110010101000111110
|
Quelle signification accorder aux informations enregistrées
?
Décoder le "message"
ci-dessus en considérant successivement :
·
que des entiers naturels sont codés sur 8 bits,
·
que des entiers naturels sont codés sur 16 bits,
On se limitera au début du "message".
|
|
| IX
Exercice Codages n°2 |
La
notion d'information utilisée en informatique est définie
comme le support de connaissances pouvant être exprimées par des
textes, des nombres, des images, des enregistrements sonores ou
vidéo...
L'ordinateur
pour représenter et mémoriser ces informations, utilise toujours
le codage binaire (qui ne contient que les 2
valeurs : 0 et 1). Quand on parle de "technologie numérique"
ou "digitale", de "son numérique" ou de "photos
numériques", cela fait référence au codage binaire qui est
alors utilisé pour représenter les informations.
L'informatique
a introduit massivement ces technologies dites "numériques",
en opposition à la "technologie analogique" selon laquelle
une grandeur (le volume d'un son par exemple) est représentée
- par analogie - par une autre grandeur continue proportionnelle
à la première ( l'intensité d'un champ magnétique par exemple,
dans un magnétophone à cassettes ).
Le numérique a l'avantage
sur l'analogique de ne pas craindre de petites altérations : un
chiffre binaire vaut 0 ou 1 mais jamais 0,99. Une information
numérisée (codée en binaire) peut ainsi être copiée à l'identique.
Un octet
contient 8 chiffres binaires (en abréviation bit, pour BInary
digiT): on a ainsi 28 = 256 valeurs différentes pour
un octet : 00000000, 00000001,
00000010, 00000011,
00000100 ...
Pour
représenter moins de 256 informations différentes, on peut donc
se contenter d'un octet : il suffit alors de choisir arbitrairement
quel code attribuer à quelle information. C'est ce qui est fait
pour les caractères. Bien que totalement arbitraire,
un codage a cependant intérêt à être partagé par le plus grand
nombre possible d'ordinateurs; en effet ce sont les codes qui
sont transmis lors de communications entre ordinateurs,
d'où l'intérêt des normalisations.
Pour
représenter plus d'informations ou des informations plus complexes,
la solution consiste à utiliser autant d'octets que nécessaire,
rangés les uns après les autres dans la mémoire de l'ordinateur.
Un écran comporte
une palette de 256 couleurs.
1) Combien faut
– il d’octet pour les représenter ?
2) Grâce à un scanner,
vous enregistrez une photo numérique d’un format 1024 par 1024
points.
N.B. 1024 octets = 1 Ko (ne pas confondre avec k qui signifie
1000 : 1 kg = 1000 g)
Quelle quantité
d’octet faut – il ?Traduire ce chiffre en méga – octet
(Mo).
3) Pour
représenter un texte écrit (sans information de mise en page),
que l'ordinateur considère comme une suite de caractères (alphabétiques,
symboles de ponctuation, espaces et passages à la ligne) sur
une page, combien faut-il d’octets ?
A quelle quantité
de pages correspond une photonumérisée ?
|
|
|